如何解释零标准差
在统计学中，标准差用于衡量样本中数值的分布情况。
我们可以使用以下公式来计算给定样本的标准差：
√ Σ( xi – x bar ) 2 / (n-1)
金子：
- Σ：表示“和”的符号
- x i :样本的第 i 个值
- x bar :样本平均值
- n：样本量
标准差值越高，样本中的值越分散。
标准差值越低，值分组得越紧密。
如果样本的标准差为零，则意味着样本中的所有值完全相同。
换句话说，价值观之间不存在差距。
以下示例显示了如何在实践中解释零标准差。
示例：如何解释零标准差
假设我们收集 10 只蜥蜴的简单随机样本并测量它们的长度（以英寸为单位）：
长度: 7, 7, 7, 7, 7, 7, 7, 7, 7, 7
样本中蜥蜴的平均长度为 7 英寸。
知道了这一点，我们可以计算该数据集的样本标准差：
- s = √ Σ( xi – x bar ) 2 / (n-1)
- s = √ ((7 – 7) 2 + (7 – 7) 2 + (7 – 7) 2 + … + (7 – 7) 2 / (10-1)
- s = √ 0 2 + 0 2 + 0 2 + … + 0 2 / 9
- s = 0
样本标准差结果为0 。
由于每只蜥蜴的长度完全相同，因此数据集中值的分布恰好为零。
现实世界中的标准差会为零吗？
现实世界的数据集的标准差完全有可能为零，但这种情况很少见。
最有可能遇到标准差为零的情况是为罕见事件收集小样本时。
例如，假设您收集某个城市一周内道路事故数量的数据。
您完全有可能收集以下数据：
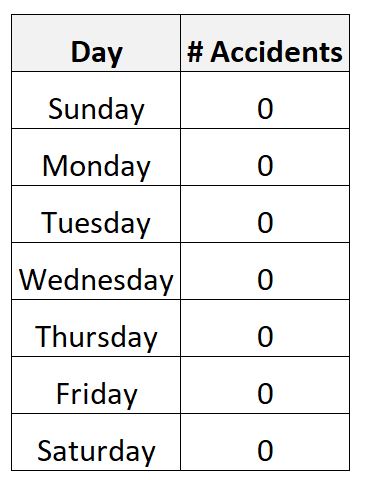
在这种情况下，每日平均事故数将为零，标准差也将为零。
或者，您可能会收集以下有关某企业 6 个月内昂贵产品月销量的数据：
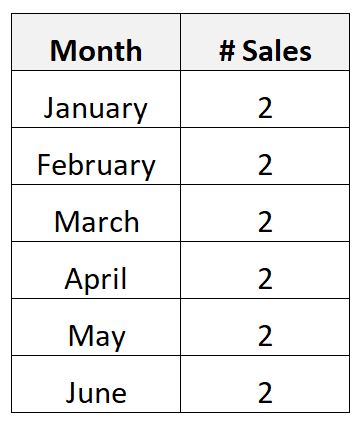
由于该产品非常昂贵，结果该公司每月只销售两件。
在此场景中，每月销售的产品的平均数量为 2，每月销售的产品的标准差为零。
每当您在实际数据集中遇到标准差为零时，只需知道这意味着数据集中的每个值都完全相同。
其他资源
以下教程提供有关统计中标准差的更多信息：
关于作者
本杰明·安德森博
大家好，我是本杰明，一位退休的统计学教授，后来成为 Statorials 的热心教师。 凭借在统计领域的丰富经验和专业知识，我渴望分享我的知识，通过 Statorials 增强学生的能力。了解更多