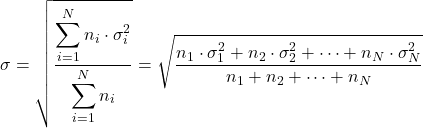标准差（或标准差）

经过本杰明·安德森博 8月 5, 2023 统计数据 0 条评论

本文解释什么是标准差，也称为标准差。您将学习如何计算标准差、分步实践示例以及用于查找任何数据样本的标准差的在线计算器。

什么是标准差（或标准差）？

标准差，也称为标准偏差，是统计离散度的度量。换句话说，标准差是表示一组统计数据分散程度的值。

因此，标准差（或标准差）用于量化总体或统计样本的离散程度。数据系列的标准差越大，表明数据越分散。也可以从另一个方向进行解释，如果标准差很低，这意味着通常数据非常接近其平均值。

计算总体的标准偏差或典型偏差时，标准偏差的符号是希腊字母 sigma (σ)。但当涉及样本标准差时，字母 s 用于表示统计测量。

在一些统计学和概率书籍中，标准差也称为标准差。

标准差（或标准差）公式

标准差（或标准差）等于数据系列偏差平方和除以观测值总数的平方根。

因此，计算标准差（或标准差）的公式为：

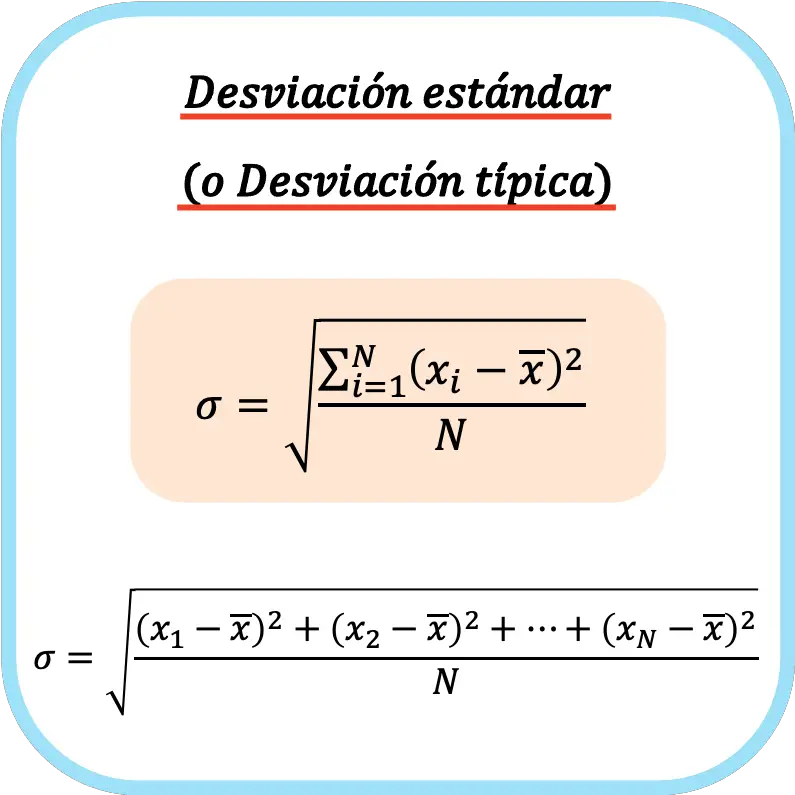
👉您可以使用下面的计算器来计算任何数据集的标准差。

总之，要找到数据集的标准差，您需要计算所有偏差（定义为数据点与算术平均值之间的差），将偏差增加到两倍，将它们全部相加，然后除以全部的。数据个数，最后取平方根。

标准差（或标准差）示例

考虑到标准差（或典型差）的定义，下面是一个分步示例，以便您可以了解如何计算数据系列的标准差。

计算以下值的标准差：3、6、2、9、4。

我们需要做的第一件事是确定样本均值。为此，我们将所有数据相加并除以观察总数（即 5）：

$\overline{x}=\cfrac{3+6+2+9+4}{5}=4,8$

我们现在使用标准差公式：

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^N(x_i-\overline{x})^2}{N}}$

我们将数据代入公式：

$\displaystyle\sigma =\sqrt{\frac{(3-4,8)^2+(6-4,8)^2+(2-4,8)^2+(9-4,8)^2+(4-4,8)^2}{5}}$

最后我们计算标准差：

$\begin{aligned}\displaystyle\sigma & = \sqrt{\frac{(-1,8)^2+1,2^2+(-2,8)^2+4,2^2+(-0,8)^2}{5}}\\[2ex]&=\sqrt{\frac{3,24+1,44+7,84+17,64+0,64}{5}}\\[2ex]&= \sqrt{\frac{30,8}{5}}=\sqrt{6,16}=2,48 \end{aligned}$

标准差（或标准差）计算器

将一组统计数据输入到下面的在线计算器中，计算其标准差（或标准差）。数据必须用空格分隔，并使用句点作为小数点分隔符输入。

分组数据的标准（或典型）偏差

要计算分组为区间的数据的标准差（或标准差） ，必须遵循以下步骤：

求分组数据的平均值。
计算分组数据的偏差。
将每个间隙平方。
将之前的每个结果乘以其间隔的频率。
将上一步获得的所有值相加。
除以观察总数。
取前一个值的平方根。所得数字是分组数据的标准差。

总之，按区间分组的数据标准差的计算公式为：

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^N\left(x_i-\overline{x}\right)^2\cdot f_i }{N}}$

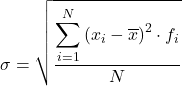
虽然通常使用上面的公式，但是也可以使用下面的代数表达式，因为可以得到相同的结果：

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^n x_i^2\cdot f_i }{N}-\overline{x}^2}$

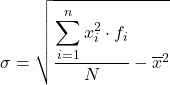
因此，您可以看到这是如何完成的，下面是对分组为区间的数据标准差的分步练习。更准确地说，将计算以下统计数据的标准差：

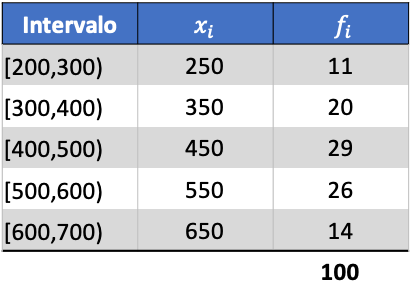
首先，我们将每个区间的班级分数乘以其频率来计算算术平均值：

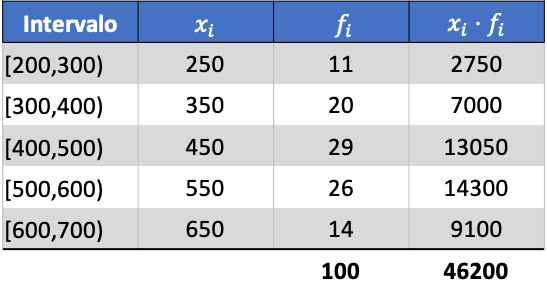
因此分组数据的平均值将是：

$\overline{x}=\cfrac{\displaystyle\sum_{i=1}^n x_i\cdot f_i}{N}=\cfrac{46200}{100}=462$

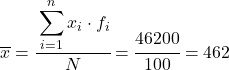
现在我们知道平均值的值，我们需要将以下三列添加到数据表中：

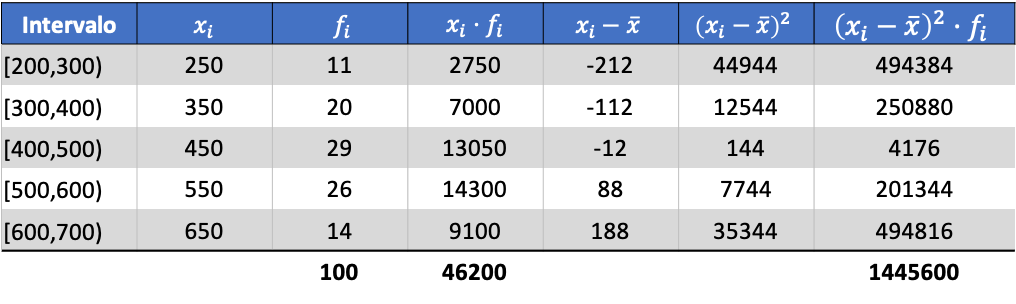
那么分组数据的标准差将是最后一列总数除以观测总数的平方根的结果：

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^N\left(x_i-\overline{x}\right)^2\cdot f_i }{N}}=\sqrt{\frac{1445600}{100}}=120,23$

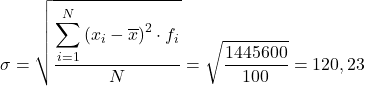
标准（或典型）偏差和方差

标准差（或典型差）与方差的关系是标准差是方差的平方根。

因此，如果我们知道数据集的方差值，我们可以通过平方根轻松计算标准差。或者相反，如果我们知道标准差，我们可以通过对该值进行平方来找到方差。

$Var(X)=\sigma^2$

事实上，方差可以简单地用平方标准差符号来表示。因此，总体方差的符号为 sigma 平方 (σ ² )，样本方差的符号为 s 平方 (s ² )。

此外，标准差和方差的概念具有相似的解释，因为两者都显示了一系列统计数据的分散性。

标准差（或标准差）的性质

标准差具有以下属性：

数据样本的标准差不能为负。

$\sigma \ge 0$

如果所有数据都相同，标准偏差将为零。

$\sigma =0$

如果将常数项添加到所有数据中，标准差值不会改变。

$\sigma (X+k)=\sigma (X)$

如果所有数据乘以一个数字，则标准差将乘以该数字的绝对值。

$\sigma (k\cdot X)=|k|\cdot \sigma (X)$

两个随机变量之和的标准差等于变量方差之和的平方根加上两个变量之间协方差的两倍。

$\sigma(X+Y)=\sqrt{Var(X)+Var(Y)+2\cdot Cov(X,Y)}$

如果我们知道不同分布的标准差 (σ _i ) 及其数据数量 (n _i )，我们可以通过应用以下公式计算总标准差：

$\displaystyle\sigma=\sqrt{\frac{\displaystyle \sum_{i=1}^N n_i\cdot \sigma_i^2}{\displaystyle \sum_{i=1}^N n_i}}=\sqrt{\frac{\displaystyle n_1\cdot \sigma_1^2+n_2\cdot \sigma_2^2+\dots +n_N\cdot \sigma_N^2}{\displaystyle n_1+n_2+\dots+n_N}}$

关于作者

本杰明·安德森博

大家好，我是本杰明，一位退休的统计学教授，后来成为 Statorials 的热心教师。凭借在统计领域的丰富经验和专业知识，我渴望分享我的知识，通过 Statorials 增强学生的能力。了解更多