树形图

本文解释什么是树形图以及它是如何制作的。因此，您将找到树结构的示例、此类图表的优点，此外还有逐步解决的练习。

什么是树？

树图，也称为概率树，是实验所有可能结果及其概率的图形表示。

因此，树形图用于绘制样本空间中所有可能的结果并计算它们的概率。

树形图的制作方式是每个结果（节点）分支成新的可能结果（分支），直到达到最终结果。

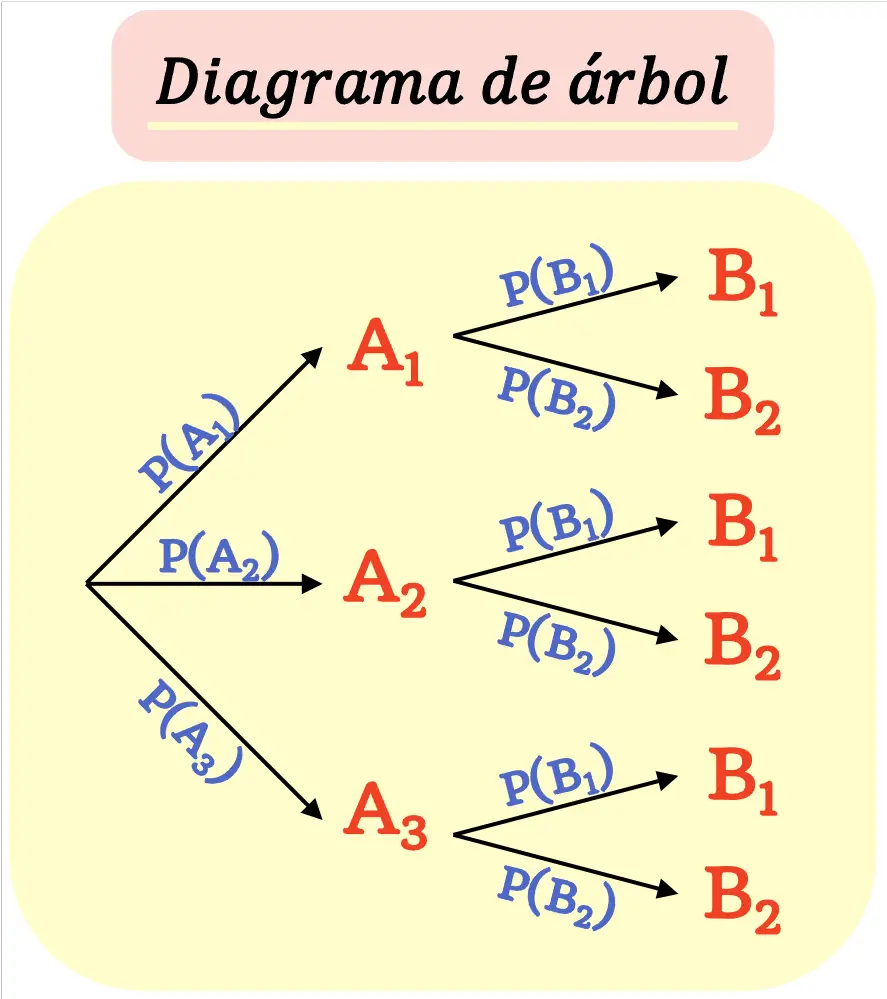
应该记住，从一个节点发出的所有分支的概率之和必须等于 1。

如何制作树形图

要创建树，必须执行以下步骤：

1. 创建树形图的第一步是为每个可能的结果绘制一个分支。这些将是第一代分支。
2. 然后，与每个事件相关的概率被添加到其相应的分支。
3. 每个第一代分支的末端是一个节点，必须从该节点表示后续可能事件的分支。
4. 与第一个分支一样，我们必须添加所表示事件的概率。
5. 重复步骤 3 和 4，直到到达最终节点，即实验的可能结束。

请注意，一个级别中的分支数量不一定必须等于不同级别中的分支数量。同样，即使在同一级别内，可能结果产生的分支数量也可能有所不同。

树的例子

现在我们已经了解了创建树形图的定义和理论，让我们逐步看一个现实世界的示例，以更好地理解这个概念。

• 构建三个独立硬币抛硬币的概率树。然后确定所有 3 次抛掷都获得正面的概率。

抽签的时候，只有两种可能的结果：正面或反面。因此，抛硬币时正面或反面出现的概率为：

一旦我们知道了可能结果的概率，我们就可以继续表示树形图。

由于抛硬币是独立的，因此每次抛硬币出现正面或反面的概率始终相同。因此，为了构建树，每次抛出时必须以相同的概率表示两个分支（头和尾）。

一旦我们制作了树，我们所要做的就是确定抛三枚硬币的概率。

因此，在这种情况下，我们必须乘以所有获得正面的概率，因为这些是引导我们到达期望结果的路径的概率。

因此，抛三次硬币得到正面的概率计算如下：

简而言之，连续 3 次正面朝上的概率为 12.5%。

解决树练习

一个村庄只有3所托儿所：60%的孩子去A托儿所，30%去B托儿所，10%去C托儿所。此外，在这3所托儿所中，55%的人是女孩。构建树并计算以下概率：

• 随机选择一个孩子时，该孩子是日托中心女孩的概率 B.
• 从任何日托中心随机选择一个孩子时，该孩子是男孩的概率。

请注意，如果所有日托机构中女孩的比例为 55%，则男孩的百分比只需减去 1 减去 0.55 即可计算得出：

现在我们知道了所有的概率，我们可以创建包含所有可能性的概率树：

因此，从日托 B 中随机选择一个女孩的概率计算如下：

另一方面，要确定在任何日托中心选择男孩的概率，我们必须首先找到每个日托中心选择男孩的概率，然后将它们加在一起：

树结构的优点

由于树结构的特点，此类统计图的优点如下：

• 树形图对于做出决策非常有用。
• 所有可能结果之间的关系可以用图形表示。
• 查找问题的根本原因非常方便。
• 使解决概率和统计问题变得更加容易。
• 树形图有助于组织想法和分析情况。