如何在 excel 中计算样本和总体变异
方差是衡量数据集中值分布的一种方法。
总体方差的计算公式为:
σ 2 = Σ ( xi – μ) 2 / N
金子:
- Σ :表示“和”的符号
- μ :人口平均值
- x i :总体中的第 i个元素
- N :人口规模
样本方差的计算公式为:
s 2 = Σ ( xi – x ) 2 / (n-1)
金子:
- x :样本平均值
- x i :样本的第 i个元素
- n :样本量
我们可以使用Excel中的VAR.S()和VAR.P()公式快速计算给定数据集的样本方差和总体方差。
以下示例展示了如何在实践中使用每个功能。
示例 1:在 Excel 中计算样本方差
下面的截图展示了如何使用VAR.S()函数计算A列中值的样本方差:
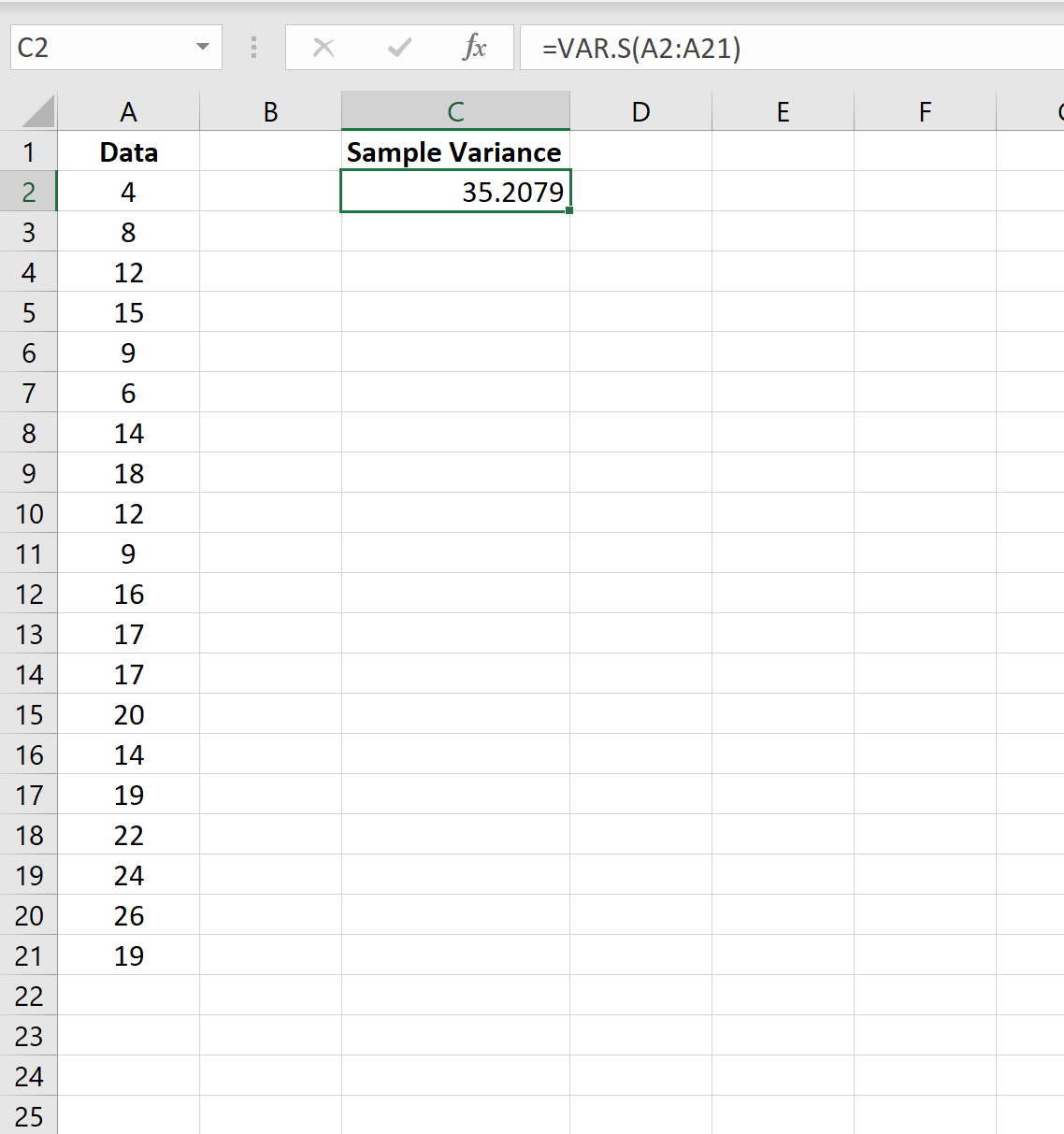
样本方差结果为35.2079 。
示例 2:在 Excel 中计算总体方差
以下屏幕截图显示了如何使用VAR.P()函数计算 A 列中的值的总体方差:
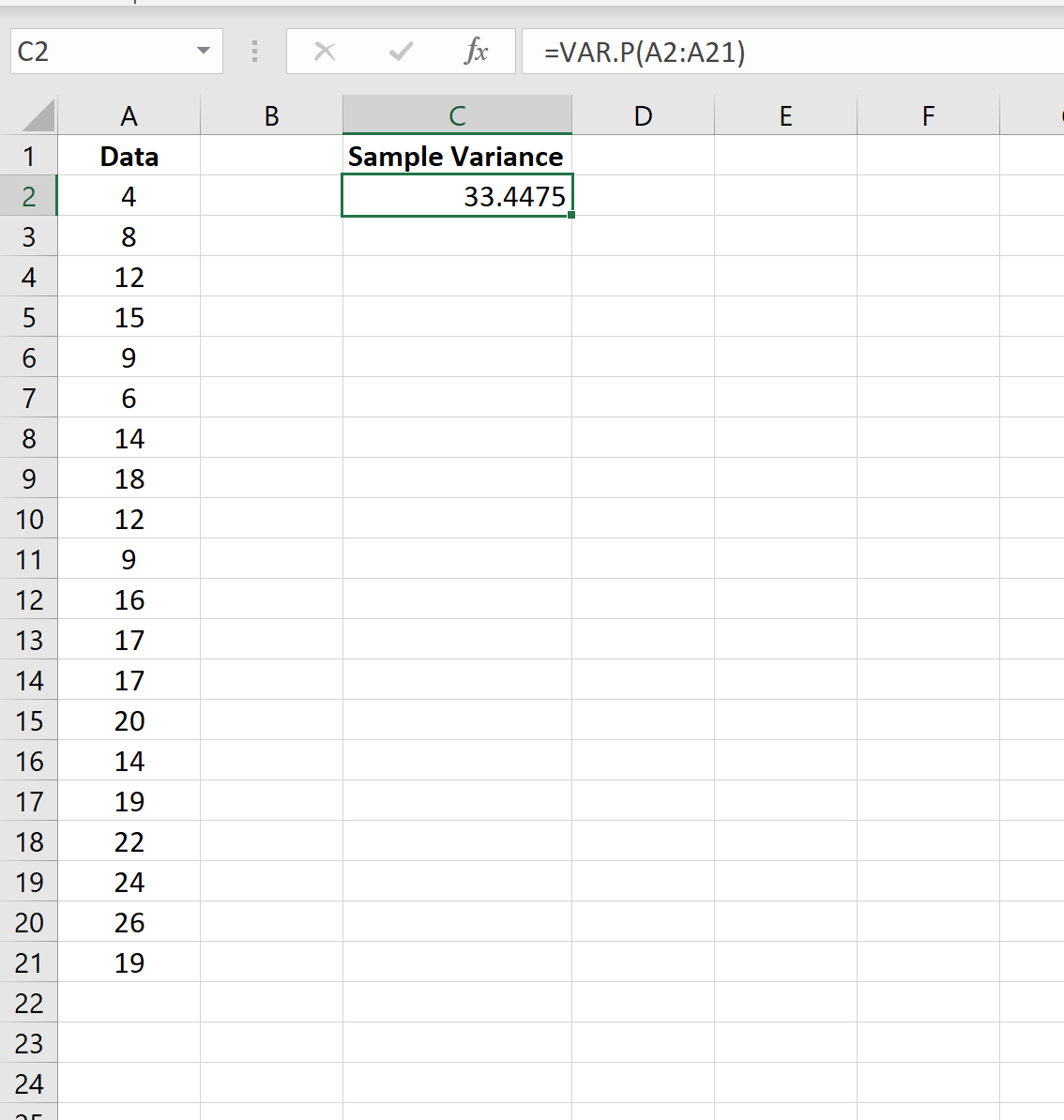
总体方差结果为33.4475 。
计算样本和总体方差的注意事项
计算样本和总体方差时请记住以下几点:
- 当您使用的数据集代表整个总体(即您感兴趣的每个值)时,您应该计算总体方差。
- 当您使用的数据集代表取自较大感兴趣总体的样本时,您应该计算样本方差。
- 数据集的样本方差总是大于同一数据集的总体方差,因为计算样本方差时存在更多不确定性,因此我们对方差的估计会更大。
其他资源
以下教程介绍了如何在 Excel 中计算其他点差指标: