样本比例

本文解释了什么是统计学中的样本比例。因此，您将了解如何计算样本比例、已解决的练习，以及样本比例和总体比例之间的差异。

样本比例是多少？

样本比例是样本中成功案例与样本量的比率。因此，要计算样本比例，必须将样本中成功的数量除以数据总数。

样本比例的符号为

。

在统计学中，进行调查时，通常并不知道所有总体数据，这就是为什么通常对代表性样本进行研究，然后将得出的结论外推到整个总体。人口。因此，样本比例用于估计整个总体的比例。下面我们将看到这是如何完成的。

比例公式示例

样本比例等于样本中成功案例的数量除以样本量。因此，样本比例的计算公式为：

金子：

• 

  是样本比例。

• 

  是样本中成功案例的数量。

• 

  是样本中数据项的总数。

样品比例计算示例

了解了样本比例的定义及其公式是什么后，本节我们将解决一个简单的示例，以便您了解样本比例是如何计算的。

• 一家公司生产一种玩具，并从另一家外部公司购买其中一个零件。然而，在他购买的批次中，出现了缺陷零件，因此他决定进行统计研究，找出完好零件的比例和缺陷零件的比例。因此，您订购了 1,000 个单位的样品，并发现了 138 个有缺陷的零件。样本中状况良好的零件所占的比例是多少？样品中缺陷零件的比例是多少？

样本中未损坏零件的数量为 1000 减去有缺陷零件的数量：

因此，为了找到样本比例，我们应用上面看到的公式：

因此，部件状况良好的样本比例为 86.2%。

另一方面，缺陷零件的比例等于一减去合格零件的比例：

因此，缺陷零件的样本比例为 13.8%。

样本比例和总体比例

人口比重是指统计人口所占的比例。也就是说，总体比例是所研究的总体的成功案例与属于该总体的所有元素之间的关系。

因此，全国比例与人口比例的区别在于，全国比例是占多数的事件的比例，而人口比例则是指涉及所有要素人口的事件的比例。

为了区分样本比例和总体比例，它们用不同的符号表示。样本比例的符号为

，而人口比例的符号是

。

一般来说，人口比例无法精确确定，因为通常并非所有人口值都是已知的。相反，通常使用具有以下公式的置信区间来估计总体比例的值：

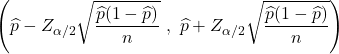
要查看如何估计人口比例，请单击以下链接：

比例抽样分布

最后，我们将了解比例抽样分布的组成，因为它是与抽样比例相关的统计概念。

首先，我们首先定义什么是抽样分布。抽样分布是考虑统计总体中所有可能样本而得出的分布。

因此，比例抽样分布是通过计算总体中每个可能样本的比例而得到的分布。也就是说，如果我们研究一个总体中所有可能的样本并计算每个样本的比例，则计算出的一组值就是样本比例的抽样分布。