概率对比比例：有什么区别？

学生在统计学中经常混淆的两个术语是概率和比例。

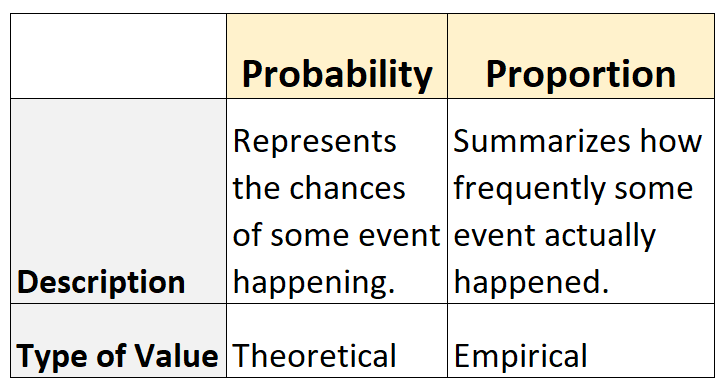
区别如下：

• 概率表示事件发生的可能性。这是理论上的。
• 该比例总结了事件实际发生的频率。这是经验性的。

我们经常用概率来谈论未来发生事件的可能性。

相反，我们经常使用比例来描述过去实际发生的事件的频率。

下面的例子说明了不同场景下概率和比例之间的差异。

示例 1：抛硬币中的概率与比例

如果我们抛一枚均匀的硬币，正面朝上的概率是 0.5 或50% 。

然而，如果我们抛一枚硬币 20 次，我们实际上可以计算出正面朝上的次数比例。例如，他在投球时可能有60%的时间都是正面朝上。

硬币正面朝上的概率是理论上的，但硬币正面朝上的次数比例是经验性的——我们实际上可以计算比例。

示例 2：掷骰子中的概率与比例

如果你掷一个六面骰子，它落在数字“4”上的概率是 1/6 或大约16.67% 。

然而，如果我们掷骰子 10 次，那么我们可以计算它落在 4 的次数的比例。例如，也许有20%的掷骰子落在“4”上。

掷出“4”的概率是理论上的，但骰子落在“4”上的次数比例是经验性的——我们实际上可以计算比例。

示例 3：概率与概率旋转器中的比例

如果我们将轮盘赌轮分成四个相等的部分（红色、蓝色、绿色和紫色），那么在任何给定的旋转中轮盘落在紫色的概率为25% 。

然而，如果我们将轮盘旋转 100 次，我们就可以计算轮盘落在紫色的次数的比例。例如，也许他有15%的旋转落在紫色上。

轮盘落在紫色上的概率是理论上的，但落在紫色上的次数比例是经验性的——我们可以实际计算比例。

示例 4：纸牌游戏中的概率与比例

在一副标准的 52 张牌中，有 4 张 Q。因此，在绘图中选择皇后的概率为 4/52 = 7.69% 。

然而，如果我们随机抽牌（并替换我们抽到的牌）50次，我们实际上可以计算出抽到皇后的次数比例。例如，也许我们在10%的抽牌中抽到了皇后。

选择皇后的概率是理论上的，但我们实际选择皇后的次数比例是经验性的——我们实际上可以计算比例。

其他资源

概率与概率：有什么区别？
全概率定律：定义和示例