如何计算概率分布的方差

概率分布告诉我们随机变量取特定值的概率。

例如，以下概率分布告诉我们某支足球队在给定比赛中进球一定数量的概率：

为了找到概率分布的方差，我们可以使用以下公式：

σ ² = Σ(x _i -μ) ² * P(x _i )

金子：

• x _i :^{第 i 个}值
• μ：分布的平均值
• P( _xi ):^{第 i 个}值的概率

例如，考虑足球队的概率分布：

足球队的平均进球数计算如下：

μ = 0*0.18 + 1*0.34 + 2*0.35 + 3*0.11 + 4*0.02 = 1.45 个进球。

然后我们可以计算方差如下：

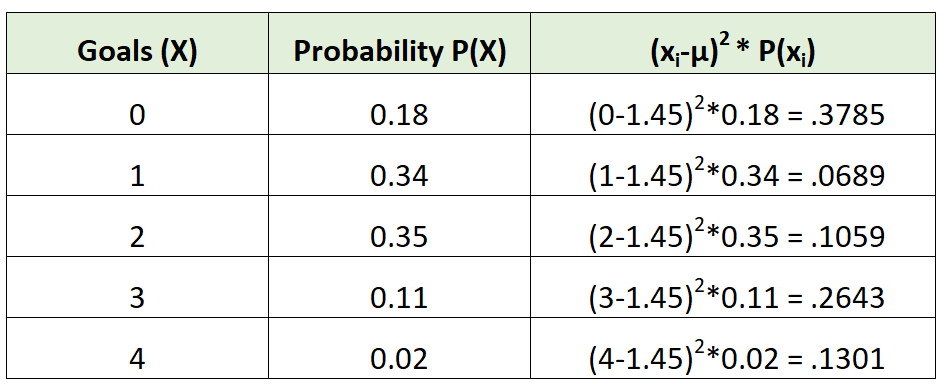
方差只是第三列中的值的总和。因此，我们将按如下方式计算：

^σ2 = 0.3785 + 0.0689 + 0.1059 + 0.2643 + 0.1301 = 0.9475

以下示例展示了如何在其他一些场景中计算概率分布的方差。

示例 1：车辆故障的变化

以下概率分布告诉我们特定车辆在 10 年内出现一定次数电池故障的概率：

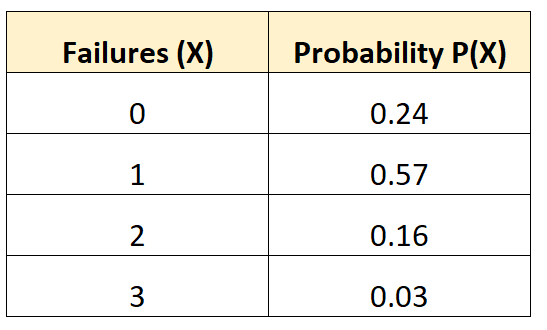
为了找到该概率分布的方差，我们首先需要计算预期失败的平均数：

μ = 0*0.24 + 1*0.57 + 2*0.16 + 3*0.03 = 0.98次失败。

然后我们可以计算方差如下：

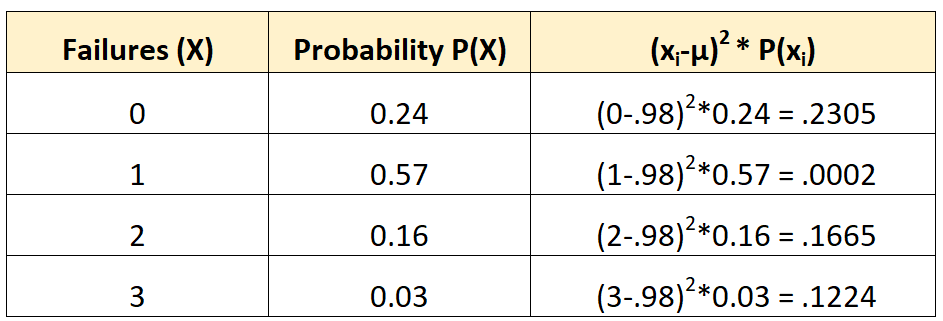
方差是第三列中的值的总和。因此，我们将按如下方式计算：

^σ2 = 0.2305 + 0.0002 + 0.1665 + 0.1224 = 0.5196

示例 2：销售变化

以下概率分布告诉我们给定卖家在下个月实现一定数量销售的概率：

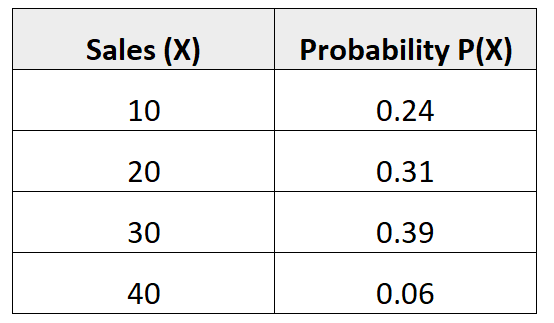
为了找到这个概率分布的方差，我们首先需要计算预期销售的平均数量：

μ = 10*0.24 + 20*0.31 + 30*0.39 + 40*0.06 = 22.7脏。

然后我们可以计算方差如下：

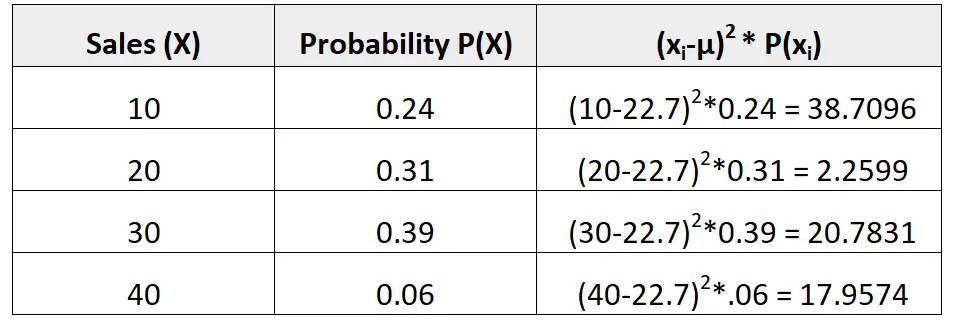
方差是第三列中的值的总和。因此，我们将按如下方式计算：

^σ2 = 38.7096 + 2.2599 + 20.7831 + 17.9574 = 79.71

请注意，我们还可以使用概率分布计算器自动计算该分布的方差：

差异为79.71 。这对应于我们手动计算的值。