为什么众数在统计学中很重要？

众数表示数据集中最常出现的值。

一个数据集可以没有模式（如果没有值重复）、一种模式或多种模式。

例如，以下数据集中的众数为 19：

数据集： 3、4、11、15、19、19、19、22、22、23、23、26

这是最常出现的值。

在统计学中，众数很重要，原因如下：

原因 1 ：这让我们知道数据集中的哪些值最常见。

原因 2 ：当无法计算平均值和中位数时，它对于查找分类数据中最常见的值很有用。

原因 3 ：它让我们了解数据集的“中心”在哪里，尽管中位数和均值更常用（正如我们将在本文后面看到的）。

以下示例在实践中说明了这些原因。

原因 1：众数告诉我们哪个值最常见

假设我们有一个包含 100,000 行的数据集，其中包含美国房屋的销售价格：

假设我们使用统计软件（如Excel 、 R 、 Python等）计算该数据集的众数，发现共有三种众数：

• 280,000 美元
• 30万美元
• 305,000 美元

这立即让我们了解了数据集中最常见的房价。

计算众数千也比查看数据行并尝试确定哪些房价最常出现要快得多。

原因 2：该模式搜索分类数据中最常见的值

假设我们有一个包含 1,000 行的数据集，它告诉我们某个社区中个人拥有的汽车的颜色：

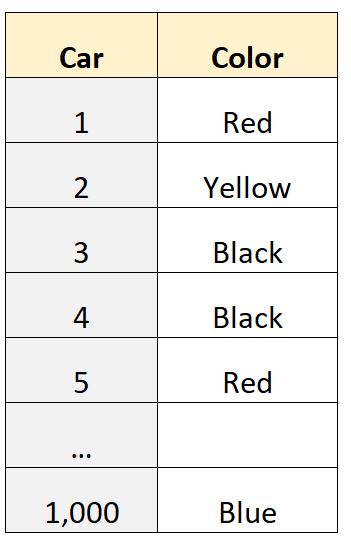
变量“颜色”是一个分类变量，这意味着这些值属于类别（“红色”、“黄色”、“黑色”等），因此我们无法计算平均值或中位数等定量值。

但是，我们可以计算众数，因为它仅代表数据集中最常见的值。

例如，我们可以使用统计软件来确定该数据集的模式为“黑色”，这告诉我们该数据集中最常见的汽车颜色是黑色。

原因3：众数让我们知道数据集的中心在哪里

该模式也被认为是集中趋势的度量，这意味着它可以让我们了解数据集的“中心”在哪里。

例如，假设我们有以下数据集，显示一个班级 20 名不同学生的考试成绩：

结果众数为82——这是最常见的考试分数。事实证明，这也很好地表明了“核心”评论评分值在此数据集中的位置。

但是，假设我们有以下考试结果数据集：

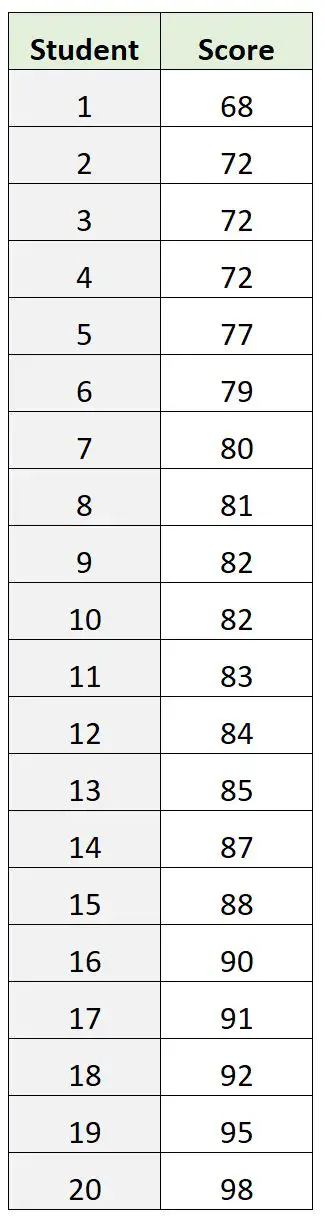
在此数据集中， 72是时尚考试分数。然而，事实证明，这并不能很好地表明考试的“核心”分数在哪里。

考试平均分是82.9分，考试中位数是82.5分，这两个分数都让我们更好地了解时尚的“中心”价值在哪里。

概括

以下是本文要点的简要总结：

• 众数表示数据集中最常出现的值。
• 当无法使用均值和中位数时，众数告诉我们分类数据中最常见的值。
• 该众数让我们了解数据集的“中心”在哪里，但与平均值或中位数相比可能会产生误导。

其他资源

以下教程提供了有关统计中的均值、中位数和众数的更多信息：

为什么平均值在统计中很重要？
为什么中位数在统计学中很重要？
具体示例：使用平均值、中位数和众数
何时使用平均值与平均值中位数：带有示例