什么是统计学中的概率质量函数 (pmf)？

概率质量函数（通常缩写为PMF ）告诉我们离散随机变量取特定值的概率。

例如，假设我们掷一次骰子。如果我们让x表示骰子落在的数字，那么x等于不同值的概率可以描述如下：

• P(X=1)：1/6
• P(X=2)：1/6
• P(X=3)：1/6
• P(X=4)：1/6
• P(X=5)：1/6
• P(X=6)：1/6

骰子落在 1 到 6 之间的任何数字上的机会均等。

以下是我们如何将这些概率写成概率质量函数：

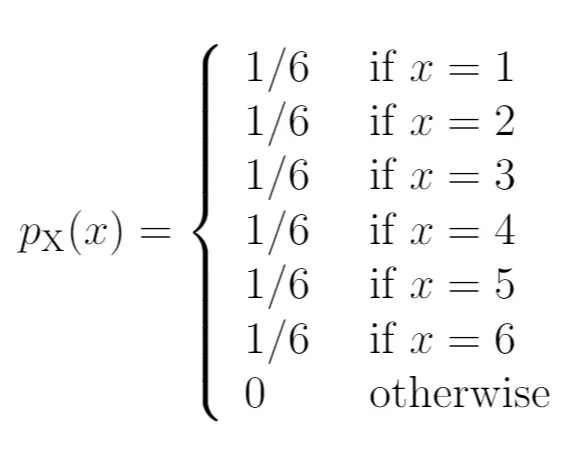
图的左侧显示了与右侧结果相关的概率：

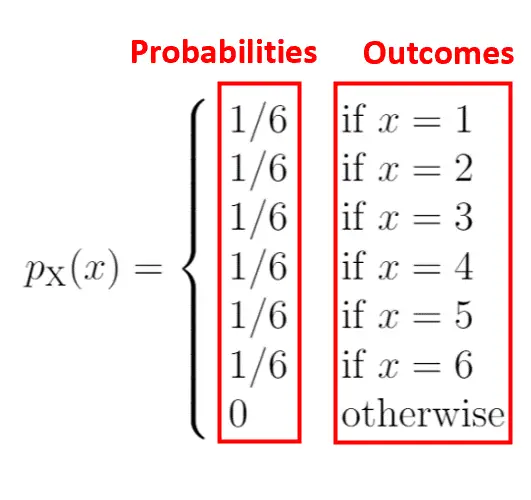
概率质量函数的一个特征是所有概率之和必须为 1。您会注意到此 PMF 满足以下条件：

概率之和 = 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 = 1。

对概率质量函数的支持是指离散随机变量可以取的值的集合。在此示例中，支持度为 {1, 2, 3, 4, 5, 6}，因为骰子的值可以采用这些值中的任何一个。

在支撑之外，PMF 值为零。例如，骰子落在“0”或“7”或“8”上的概率为零，因为这些数字都不包含在括号中。

实践中的概率质量函数

实践中概率质量函数的两个最常见的例子涉及二项式分布和泊松分布。

二项分布

如果随机变量X服从二项式分布，则X = k成功的概率可以通过以下公式求出：

P(X=k) = _n C _k * p ^k * (1-p) ^nk

金子：

• n：试验次数
• k：成功次数
• p：给定试验的成功概率
• _n C _k ：在n次试验中获得k次成功的方法数

例如，假设我们抛硬币 3 次。我们可以使用上面的公式来确定这 3 次抛掷中获得 0、1、2 和 3 次正面朝上的概率：

• P(X=0) = ₃ C ₀ * 0.5 ⁰ * (1-0.5) ^3-0 = 1 * 1 * (0.5) ³ = 0.125
• P(X=1) = ₃ C ₁ * 0.5 ¹ * (1-0.5) ^3-1 = 1 * 1 * (0.5) ² = 0.375
• P(X=2) = ₃ C ₂ * 0.5 ² * (1-0.5) ^3-2 = 1 * 1 * (0.5) ¹ = 0.375
• P(X=3) = ₃ C ₃ * 0.5 ³ * (1-0.5) ^3-3 = 1 * 1 * (0.5) ⁰ = 0.125

鱼类分布

如果随机变量X服从泊松分布，则X = k成功的概率可以通过以下公式求出：

P(X=k) = λ ^k * e ^{– λ} / k!

金子：

• λ：特定时间间隔内发生的平均成功次数
• k：成功次数
• e：约等于 2.71828 的常数

例如，假设某家医院平均每小时分娩 2 名婴儿。我们可以使用上面的公式来确定经历0、1、2、3次出生等的概率。在给定的时间内：

• P(X=0) = 2 ⁰ * e ^{– 2} / 0！ = 0.1353
• P(X=1) = 2 ¹ * e ^{– 2} / 1！ = 0.2707
• P(X=2) = 2 ² * e ^{– 2} / 2！ = 0.2707
• P(X=3) = 2 ³ * e ^{– 2} / 3！ = 0.1805

查看 PMF

我们经常用条形图来可视化概率质量函数。

例如，以下条形图显示了与上例中描述的泊松分布的每小时出生数相关的概率：

请注意，出生次数可以延伸至无穷大，但在 10 次之后概率会变得非常小，以至于您甚至无法在条形图上看到它们。

PMF 的属性

概率质量函数具有以下属性：

1. 所有的概率都是正支持的。例如，骰子落在 1 和 6 之间的概率为正，而所有其他结果的概率为零。

2. 所有结果的概率都在 0 到 1 之间。例如，骰子落在 1 到 6 之间的概率是 1/6，即每个结果为 0.1666666。

3. 所有概率之和必须等于1。例如，骰子落在某个数字上的概率之和为1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1。 /6 = 1。

其他资源

什么是随机变量？
CDF 或 PDF：有什么区别？
二项分布简介
泊松分布简介