如何在 ti-84 计算器上计算正态概率

正态分布是所有统计中最常用的分布。本教程介绍如何在 TI-84 计算器上使用以下函数来查找正态分布概率：

Normalpdf(x, μ, σ)返回与正态 pdf 相关的概率，其中：

• x = 个体值
• μ = 总体平均值
• σ = 总体标准差

normalcdf(lower_x, upper_x, μ, σ)返回与两个值之间的正态 cdf 相关的累积概率。

金子：

• lower_x = 较低的个人价值
• upper_x = 个体值上限
• μ = 总体平均值
• σ = 总体标准差

在 TI-84 计算器上，可以通过按2nd然后按vars来访问这两个函数。这将带您进入DISTR屏幕，您可以在其中使用normalpdf()和normalcdf() ：

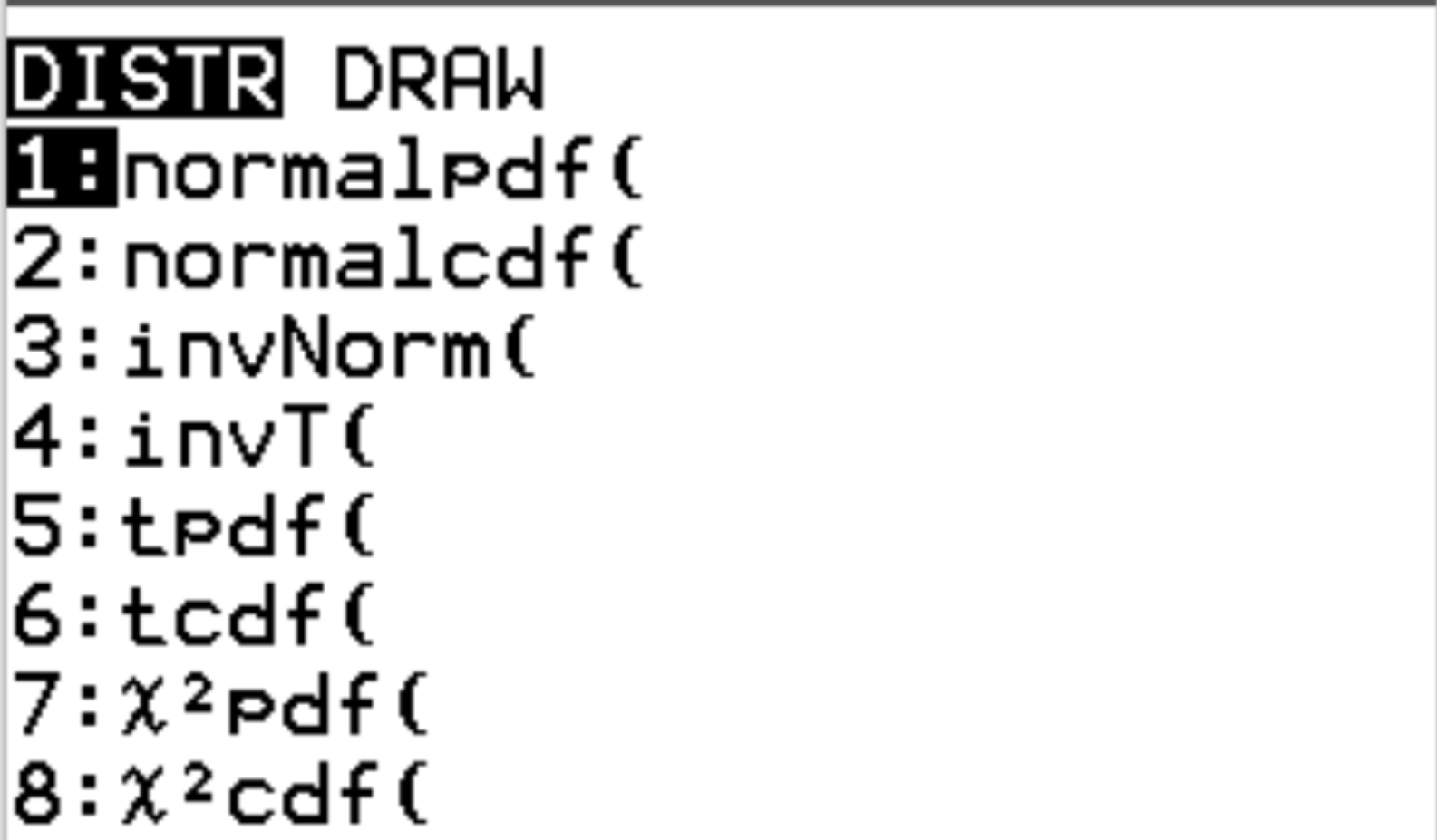
以下示例说明了如何使用这些函数来回答不同的问题。

示例 1：大于 x 的正态概率

问题：对于平均值 = 40、标准差 = 6 的正态分布，求某个值大于 45 的概率。

答案：使用normalcdf(x, 10000, μ, σ)函数：

正常 CDF(45, 10000, 40, 6) = 0.2023

注意：由于该函数需要 upper_x 值，因此我们只需使用 10,000。

示例 2：小于 x 的正态概率

问题：对于平均值 = 100、标准差 = 11.3 的正态分布，求某个值小于 98 的概率。

答案：使用normalcdf(-10000, x, μ, σ)函数：

正常CDF(-10000, 98, 100, 11.3) = 0.4298

注意：由于该函数需要 lower_x 值，因此我们只需使用 -10000。

示例 3：两个值之间的正态概率

问题：对于平均值 = 50、标准差 = 4 的正态分布，求某个值在 48 到 52 之间的概率。

答案：使用normalcdf(smaller_x, Larger_x, μ, σ)函数

正常 CDF(48, 52, 50, 4) = 0.3829

示例 4：除了两个值之外的正态概率

问题：对于均值 = 22、标准差 = 4 的正态分布，求某个值小于 20 或大于 24 的概率。

答案：使用函数normalcdf(-10000,small_x,μ,σ)+normalcdf(larger_x,10000,μ,σ)

正常CDF(-10000, 20, 22, 4) + 正常CDF(24, 10000, 22, 4) = 0.6171