比例假设检验
本文解释了统计学中假设检验的比例。因此,您将找到该比例的假设检验公式,此外,您还将找到一个分步练习,以充分理解它是如何完成的。
什么是比例假设检验?
比例假设检验是一种统计方法,用于确定是否拒绝总体比例的原假设。
因此,根据假设检验统计量的比例和显着性水平的值,拒绝或接受原假设。
请注意,假设检验也可称为假设对比、假设检验或显着性检验。
比例的假设检验公式
比例的假设检验统计量等于样本比例的差值减去比例的建议值除以比例的标准差。
因此,该比例的检验假设公式为:

金子:
-

是该比例的假设检验统计量。
-

是样本比例。
-

是建议比例的值。
-

是样本大小。
-

是比例的标准差。
请记住,计算比例的假设检验统计量是不够的,但必须解释结果:
- 如果该比例的假设检验是双向的,则当统计量的绝对值大于临界值 Z α/2时,将拒绝原假设。
- 如果该比例的假设检验与右尾匹配,且统计量大于临界值 Z α ,则拒绝原假设。
- 如果比例的假设检验与左尾匹配,且统计量小于临界值 -Z α ,则拒绝原假设。
![Rendered by QuickLaTeX.com \begin{array}{l}H_1: p\neq p_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |Z|>Z_{\alpha/2} \text{ se rechaza } H_0\\[3ex]H_1: p> p_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z>Z_{\alpha} \text{ se rechaza } H_0\\[3ex]H_1: p< p_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z<-Z_{\alpha} \text{ se rechaza } H_0\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-7d5bd583532769e3014286e8ffd94c9f_l3.png)
请记住,可以从正态分布表中轻松获得临界值。
比例假设检验示例
一旦我们了解了比例假设检验的定义及其公式是什么,我们将解决一个例子来更好地理解这个概念。
- 据其制造商称,针对特定疾病的药物有 70% 的有效性。在实验室中,我们测试了这种药物的有效性,因为研究人员认为比例不同。为此,该药物在 1,000 名患者样本上进行了测试,并治愈了 641 人。对总体比例进行假设检验,显着性水平为 5%,以拒绝或不拒绝研究人员的假设。
在这种情况下,人口比例的假设检验的原假设和备择假设为:
![Rendered by QuickLaTeX.com \begin{cases}H_0: p=0,70\\[2ex] H_1:p\neq 0,70 \end{cases}](https://statorials.org/wp-content/ql-cache/quicklatex.com-f7da8281eeecc022e2ec7daea6a9756e_l3.png)
样本中被药物治愈的人数比例为:
![]()
我们通过应用上面的公式来计算该比例的假设检验统计量:
![Rendered by QuickLaTeX.com \begin{aligned} \displaystyle Z&=\frac{\widehat{p}-p}{\displaystyle\sqrt{\frac{p(1-p)}{n}}}\\[2ex]Z&=\frac{0,641-0,70}{\displaystyle\sqrt{\frac{0,70\cdot (1-0,70)}{1000}}} \\[2ex] Z&=-4,07\end{aligned}}](https://statorials.org/wp-content/ql-cache/quicklatex.com-e689388b0a73e91c1e3d8812c2c4c42a_l3.png)
另一方面,由于显着性水平为 0.05 并且这是双尾假设检验,因此检验的临界值为 1.96。
![]()
总之,检验统计量的绝对值大于临界值,因此我们拒绝原假设并接受备择假设。
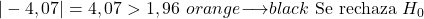 ➤请参阅:均值的假设检验
➤请参阅:均值的假设检验
两个样本比例的假设检验
对两个样本比例的假设检验用于拒绝或接受两个不同总体的比例相等的零假设。
因此,两个样本比例的假设检验的原假设始终为:
![]()
虽然替代假设可以是以下三个选项之一:
*** QuickLaTeX cannot compile formula:
\begin{array}{l}H_1:p_1\neq p_2\\[2ex]H_1:p_1>p_2\\[2ex]H_1:p_1 The combined ratio of the two samples is calculated as follows:[latex]p=\cfrac {x_1+x_2}{n_1+n_2}
*** Error message:
Missing $ inserted.
leading text: \begin{array}{l}
Please use \mathaccent for accents in math mode.
leading text: ...H_1:p_1>p_2\\[2ex]H_1:p_1 The combined ratio
Please use \mathaccent for accents in math mode.
leading text: ...\[2ex]H_1:p_1 The combined ratio of the two
Please use \mathaccent for accents in math mode.
leading text: ...combined of the two samples is calculated
\begin{array} on input line 8 ended by \end{document}.
leading text: \end{document}
Improper \prevdepth.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
Missing } inserted.
leading text: \end{document}
Missing \cr inserted.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
You can't use `\end' in internal vertical mode.
两个样本比例的假设检验统计量的计算公式为:
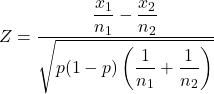
金子:
-

是两个样本比例的假设检验统计量。
-
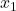
是样本 1 中的结果数。
-
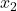
是样本 2 中的结果数。
-

是样本量 1。
-

是样本量 2。
-

是两个样本的总比例。
k 个样本比例的假设检验
在关于 k 个样本比例的假设检验中,目标是确定不同总体的所有比例是否相等,或者相反,是否存在不同的比例。因此,本例中的原假设和备择假设为:
![Rendered by QuickLaTeX.com \begin{cases}H_0: \text{Todas las proporciones son iguales}\\[2ex] H_1: \text{No todas las proporciones son iguales} \end{cases}](https://statorials.org/wp-content/ql-cache/quicklatex.com-77d7e13b427dd927953473a6bfbe9a55_l3.png)
在这种情况下,所有样本的组合比例计算如下:
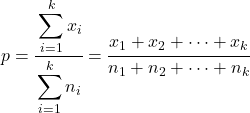
查找 k 个样本比例的假设检验统计量的公式为:
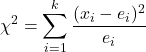
![]()
金子:
-

是 k 个样本比例的假设检验统计量。在这种情况下,统计量服从卡方分布。
-

是样本 i 中的结果数。
-

是样本大小 i。
-

是所有样本的总比例。
-

是样本 i 的预期命中数。它是通过乘以组合比例来计算的

按样本量

。