比例差异抽样分布

本文解释了比例抽样分布的差异是什么以及它在统计中的用途。还提出了比例抽样分布公式的差异和逐步解决的练习。

比例差异的抽样分布是怎样的？

比例抽样分布差异是通过计算来自两个不同总体的所有可能样本的抽样比例之间的差异而得到的分布。

即获取比例差异的抽样分布的过程是，首先从两个不同总体中提取所有可能的样本，其次确定每个提取样本的比例，最后确定所有样本之间的差异。比例之差的比例。两个人口。这样执行这些操作后得到的结果集合就形成了比例差异的抽样分布。

在统计学中，比例抽样分布差用于计算随机抽取的两个样本的样本比例之差接近总体比例之差的概率。

比例差抽样分布公式

比例抽样分布差异所选择的样本由二项式分布定义，因为出于实际目的，比例是成功案例与观测总数的比率。

然而，由于中心极限定理，二项式分布可以近似为正态概率分布。因此，比例差异的抽样分布可以近似为具有以下特征的正态分布：

注：比例差异的抽样分布只能近似于正态分布，如果

,

,

,

,

和

。

因此，由于比例差的抽样分布可以近似为正态分布，因此比例差的抽样分布统计量的计算公式为：

金子：

• 

  是样本比例 i。

• 

  是人口 i 的比例。

• 

  是群体 i 失败的概率，

  

  。

• 

  是样本大小 i。

• 

  是由标准正态分布 N(0,1) 定义的变量。

该公式类似于比例差异的假设检验公式。

比例差抽样分布的具体例子

在了解了比例差分抽样分布的定义及其公式是什么之后，您可以看到下面逐步解决的示例来完成对概念的理解。

• 您想要分析两个生产工厂的精度，一个工厂的生产方式是，所生产的零件中只有 5% 有缺陷，而另一家工厂的缺陷零件百分比为 8%。如果我们从第一个工厂抽取 200 个零件样本，从第二个工厂抽取 280 个零件样本，那么第一个生产工厂的缺陷百分比大于第二个工厂的缺陷百分比的概率是多少？生产？

为了了解问题的所有数据，我们首先计算每个工厂的良品率：

如果第一家工厂的缺陷率大于第二家工厂的缺陷率，则意味着以下等式成立：

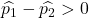
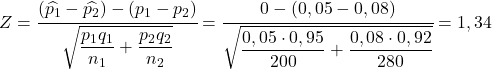
因此，第一家工厂的缺陷率大于第二家工厂的缺陷率的概率相当于变量Z大于1.34的概率：

正态分布表中查找对应的概率就已经解决了问题：

➤请参阅：均值差异的抽样分布