如何找到 z 分数右侧的区域（附示例）

在统计学中， z 分数告诉我们给定值与总体平均值的标准差有多少。

我们使用以下公式计算给定值的 z 分数：

z = (x – μ) / σ

金子：

• x ：个人数据的值
• μ ：人口平均值
• σ ：总体标准差

要查找给定 z 分数右侧的正态分布下的面积，我们可以使用以下两种方法之一：

1.使用 z 表。

2.使用Z 分数计算器右侧的框。

以下示例展示了如何在实践中使用每种方法。

示例 1：负 Z 分数右侧的区域

某种海豚的体重呈正态分布，平均值 μ = 300 磅，标准差 σ = 15 磅。体重超过 284 磅的海豚大约占百分之多少？

体重 284 磅的 z 分数计算如下： z = (284 – 300) / 15 = -1.07

我们可以使用两种方法之一来查找此 z 分数右侧的区域：

方法1：使用z表。

要找到 z 分数右侧的区域，我们可以简单地在 z 表中查找值-1.07 ：

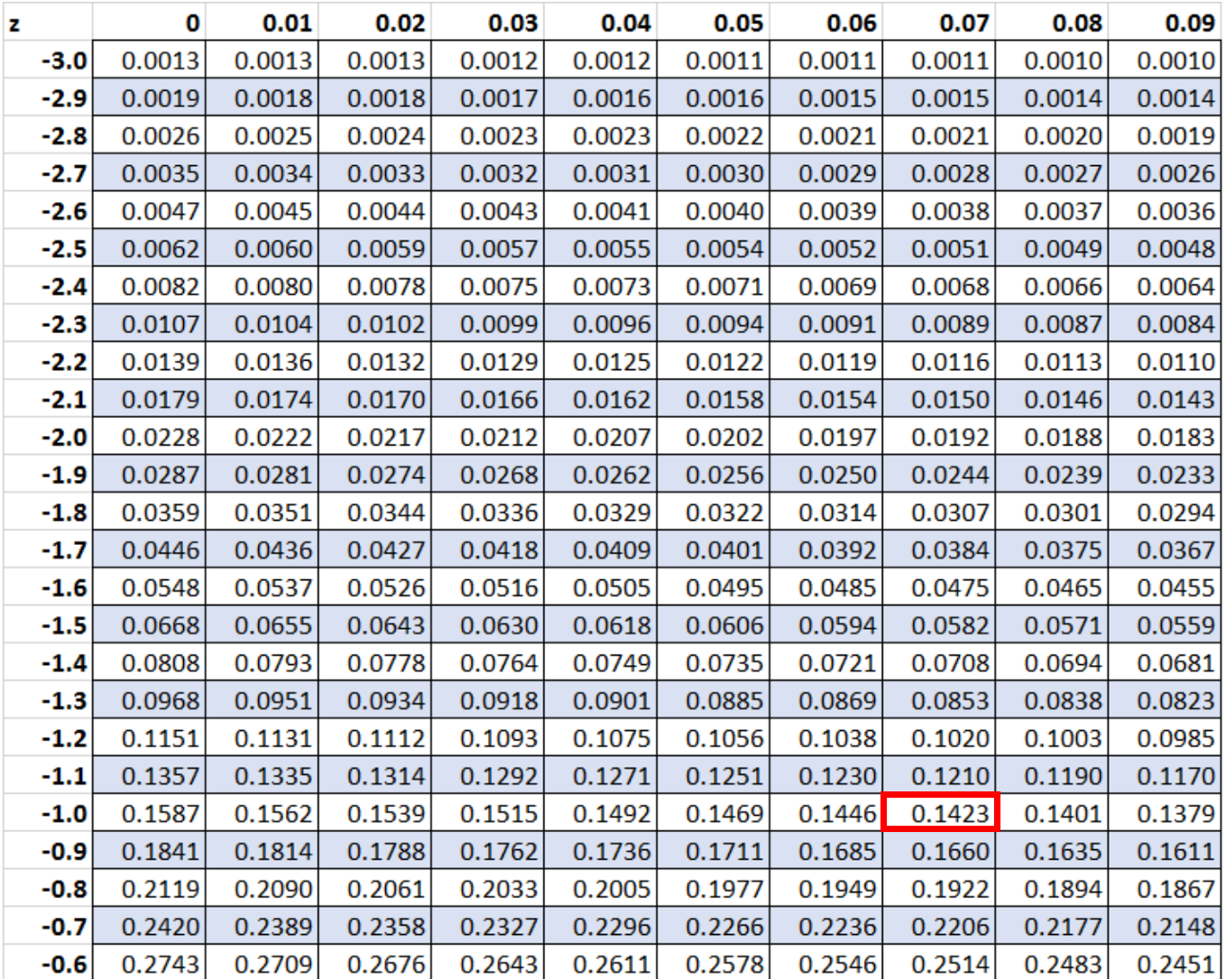
这表示 z = -1.07 左侧的区域。因此，右侧面积计算如下： 1 – 0.1423 = 或0.8577 。

应用到我们的场景中，这意味着大约85.77%的海豚体重超过 284 磅。

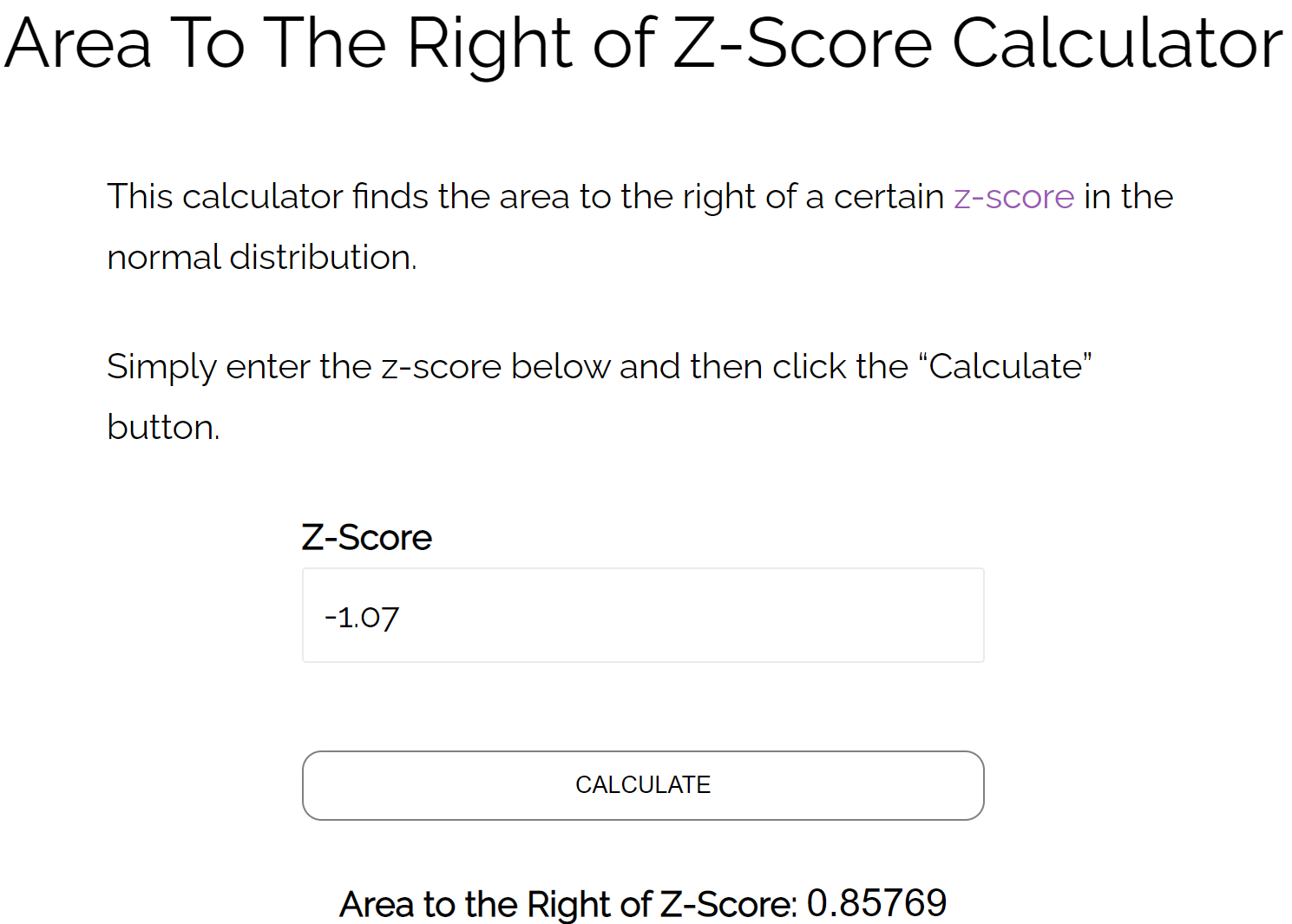
方法 2：使用 Z 分数计算器右侧的框

我们还可以使用Z 分数计算器右侧的面积来发现 z = -1.07 右侧的面积为0.8577 。

示例 2：正 Z 分数右侧的区域

给定考试的分数呈正态分布，平均值 μ = 85，标准差 σ = 8。考试成绩高于 87 分的学生大约占多少百分比？

考试成绩 87 分的 z 分数计算如下：z = (87 – 85) / 8 = 0.25。

我们可以使用两种方法之一来查找此 z 分数右侧的区域：

方法1：使用z表。

要找到 z 分数右侧的区域，我们可以简单地在 z 表中查找值0.25 ：

表示 z = 0.25 左侧的面积。因此，右侧面积计算如下： 1 – 0.5987 = 0.4013 。应用到我们的场景中，这意味着大约40.13%的学生在这次考试中得分高于 87 分。

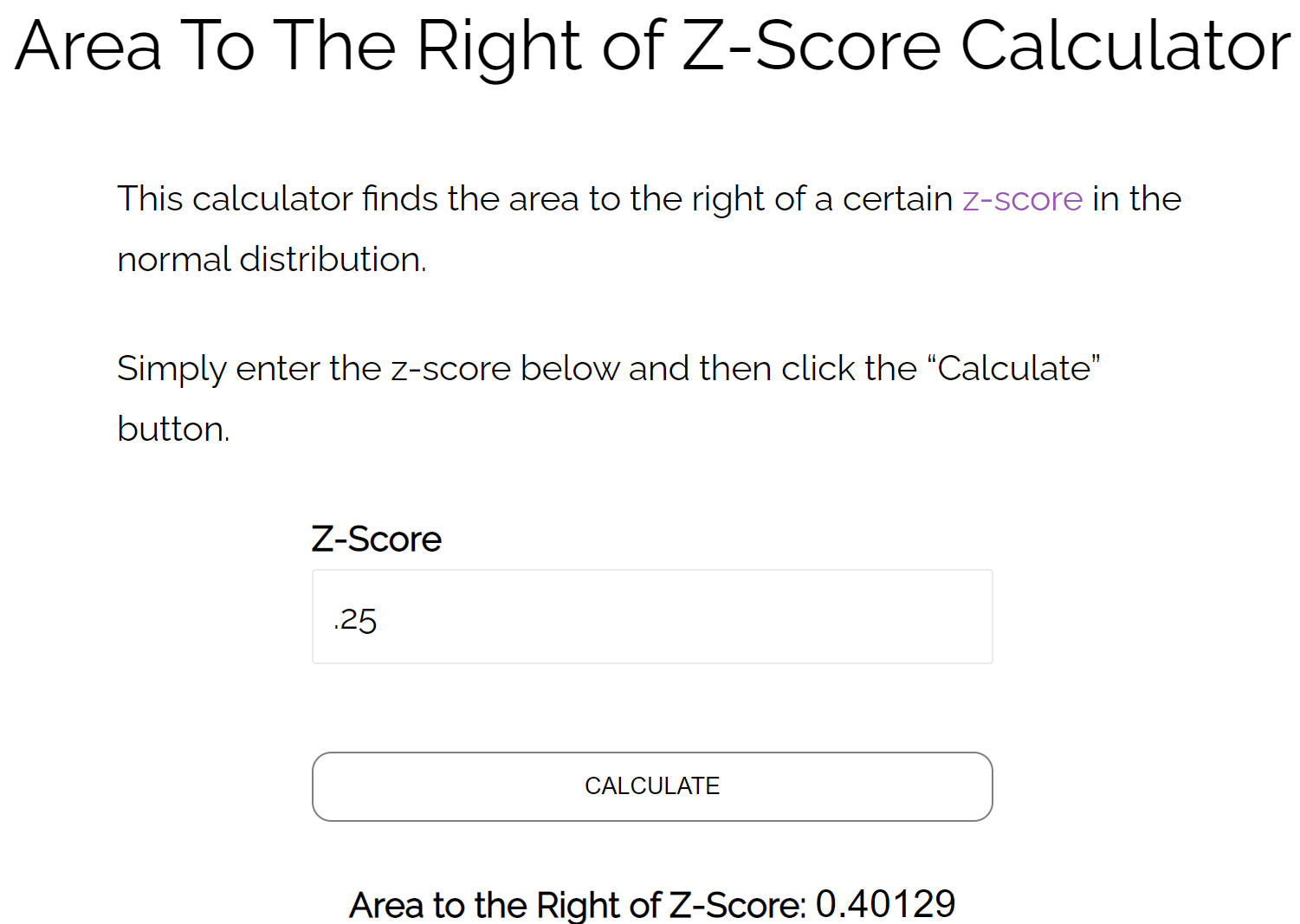
方法 2：使用 Z 分数计算器右侧的框

我们还可以使用Z 分数计算器右侧的面积来发现 z = 0.25 右侧的面积为0.4013 。

其他资源

以下教程提供了有关使用 z 分数的更多信息：

如何找到 Z 分数左侧的区域
如何查找给定区域的 Z 分数
什么被认为是好的 Z 分数？
如何根据 Z 分数手动计算 P 值