如何在给定平均值和标准差的情况下找到概率

我们可以使用以下过程来查找正态分布随机变量的概率

第 1 步：找到 z 分数。

z 分数告诉您单个数据值与平均值的标准差有多少。计算方法如下：

z 分数 = (x – μ) / σ

金子：

• x：单个数据值
• μ：总体平均值
• σ：总体标准差

第 2 步：找到与 z 分数相对应的概率。

一旦我们计算出了z分数，我们就可以在z表中找到它对应的概率。

以下示例展示了如何在不同场景中使用此流程。

示例 1：小于某个值的概率

某项测试的分数呈正态分布，平均值 μ = 82，标准差 σ = 8。给定学生在测试中得分低于 84 的概率是多少？

第 1 步：找到 z 分数。

首先，我们将找到与 84 分相关的 z 分数：

z 分数 = (x – μ) / σ = (84 – 82) / 8 = 2/8 = 0.25

步骤2：利用z表求出对应的概率。

接下来，我们将在 z 表中查找值0.25 ：

给定学生得分低于 84 分的概率约为59.87% 。

示例 2：大于某个值的概率

某种企鹅的身高呈正态分布，平均值为 μ = 30 英寸，标准差为 σ = 4 英寸。如果我们随机选择一只企鹅，它身高超过 28 英寸的概率是多少？

第 1 步：找到 z 分数。

首先，我们将找到与 28 英寸高度相关的 z 分数。

得分 z = (x – μ) / σ = (28 – 30) / 4 = -2 / 4 = -0.5

步骤2：利用z表求出对应的概率。

接下来我们将寻找值-0.5  在表z中：

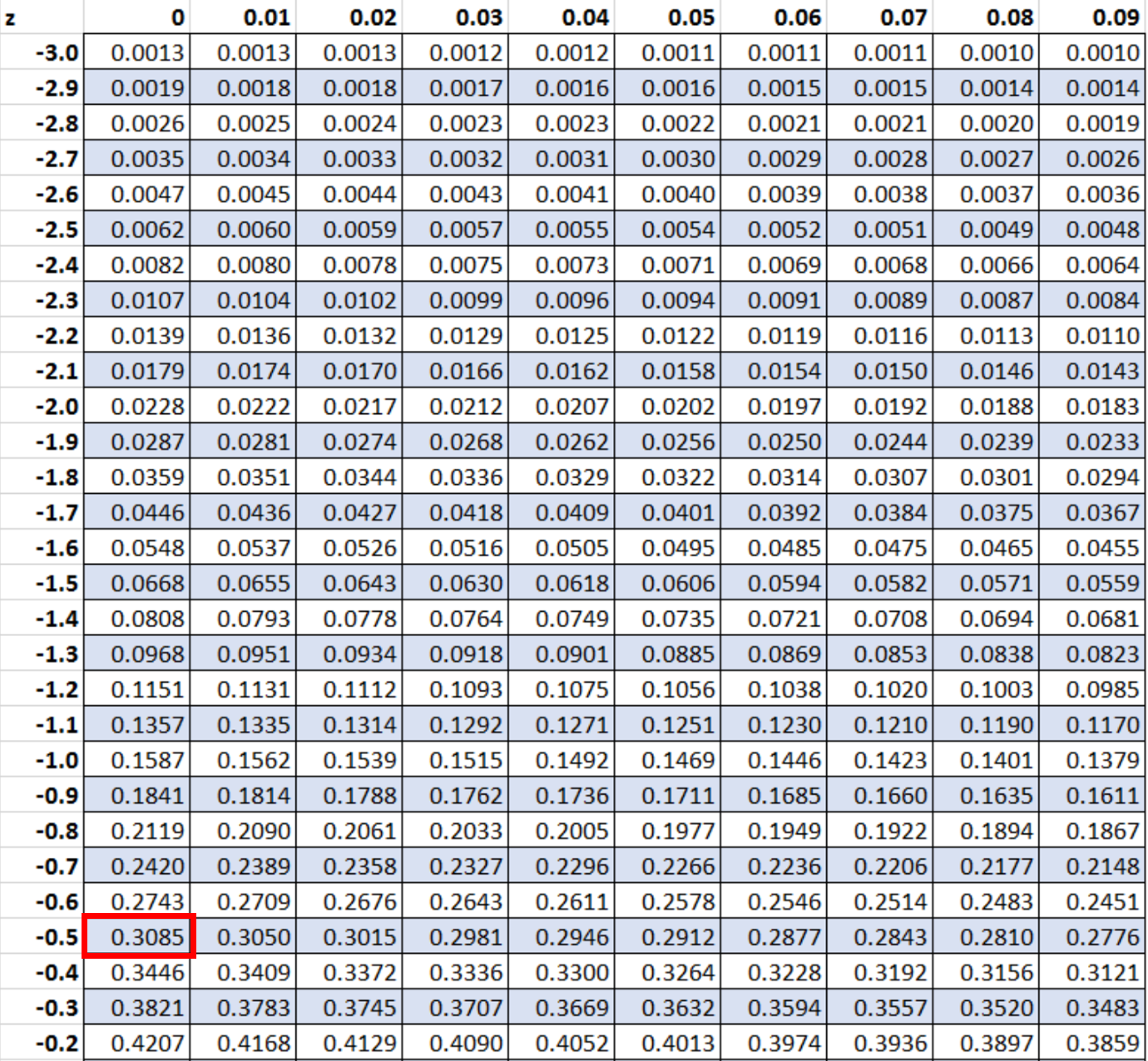
与 z 分数 -0.5 对应的值为 0.3085。这代表企鹅身高低于 28 英寸的概率。

然而，由于我们想知道企鹅身高超过 28 英寸的概率，因此我们需要从 1 中减去该概率。

因此，企鹅身高超过 28 英寸的概率为：1 – 0.3085 = 0.6915 。

示例 3：两个值之间的概率

某种海龟的体重呈正态分布，平均值为 μ = 400 磅，标准差为 σ = 25 磅。如果我们随机选择一只乌龟，它的重量在 410 到 425 磅之间的概率是多少？

第 1 步：找到 z 分数。

首先，我们将找到与 410 本书和 425 本书相关的 z 分数

z 分数 410 = (x – μ) / σ = (410 – 400) / 25 = 10/25 = 0.4

z 分数 425 = (x – μ) / σ = (425 – 400) / 25 = 25 / 25 = 1

步骤2：利用z表求出对应的概率。

首先，我们将寻找值0.4  在表z中：

接下来我们将寻找值1  在表z中：

接下来，我们将从较大的值中减去较小的值： 0.8413 – 0.6554 = 0.1859 。

因此，随机选择一只乌龟体重在 410 磅到 425 磅之间的概率为18.59% 。

其他资源

如何根据 Z 分数手动计算 P 值
如何将 Z 分数转换为原始分数
如何查找给定区域的 Z 分数