如何计算泊松置信区间（逐步）

泊松分布是一种概率分布，用于对固定时间间隔内发生的一定数量的事件的概率进行建模，其中已知事件独立发生且平均速率恒定。

虽然了解泊松过程的平均出现次数很有用，但了解平均出现次数的置信区间可能更有用。

例如，假设我们随机一天在呼叫中心收集数据，发现每小时平均呼叫次数为 15 个。

由于我们只收集了一天的数据，因此我们无法确定呼叫中心全年平均每小时接到 15 个呼叫。

但是，我们可以使用以下公式来计算每小时平均调用次数的置信区间：

泊松置信区间公式

置信区间 = [0.5*X ² _{2N, α/2} , 0.5*X ² _{2(N+1), 1-α/2} ]

金子：

• X ² : 卡方临界值
• N：观察到的事件数
• α：显着性水平

以下分步示例说明了如何在实践中计算 95% 泊松置信区间。

第 1 步：对观察到的事件进行计数

假设我们计算呼叫中心每小时的平均呼叫次数为 15。因此， N = 15 。

由于我们计算的是 95% 置信区间，因此我们将在以下计算中使用α = 0.05 。

步骤 2：找到置信区间的下限

置信区间的下限计算如下：

• 下限=0.5*X ² _2N,α/2
• 下限 = 0.5*X ² _{2(15), 0.975}
• 下限 = 0.5*X ² _{30, 0.975}
• 下限=0.5*16.791
• 下限 = 8.40

注：我们使用卡方临界值计算器计算 X ² _{30, 0.975} 。

步骤 3：找到置信区间的上限

置信区间的上限计算如下：

• 上限=0.5*X ² _{2(N+1), 1-α/2}
• 上限=0.5*X ² _{2(15+1), 0.025}
• 上限 = 0.5*X ² _{32, 0.025}
• 上限=0.5*49.48
• 上限 = 24.74

注意：我们使用卡方临界值计算器来计算 X ² _32.0.025 。

第 4 步：找到置信区间

使用之前计算的下限和上限，我们的 95% 泊松置信区间结果为：

• 95% CI = [8.40, 24.74]

这意味着我们 95% 确信呼叫中心每小时收到的实际平均呼叫数在 8.40 到 24.74 次呼叫之间。

奖励：鱼置信区间计算器

请随意使用此泊松置信区间计算器来自动计算泊松置信区间。

例如，以下是如何使用此计算器查找我们刚刚手动计算的泊松置信区间：

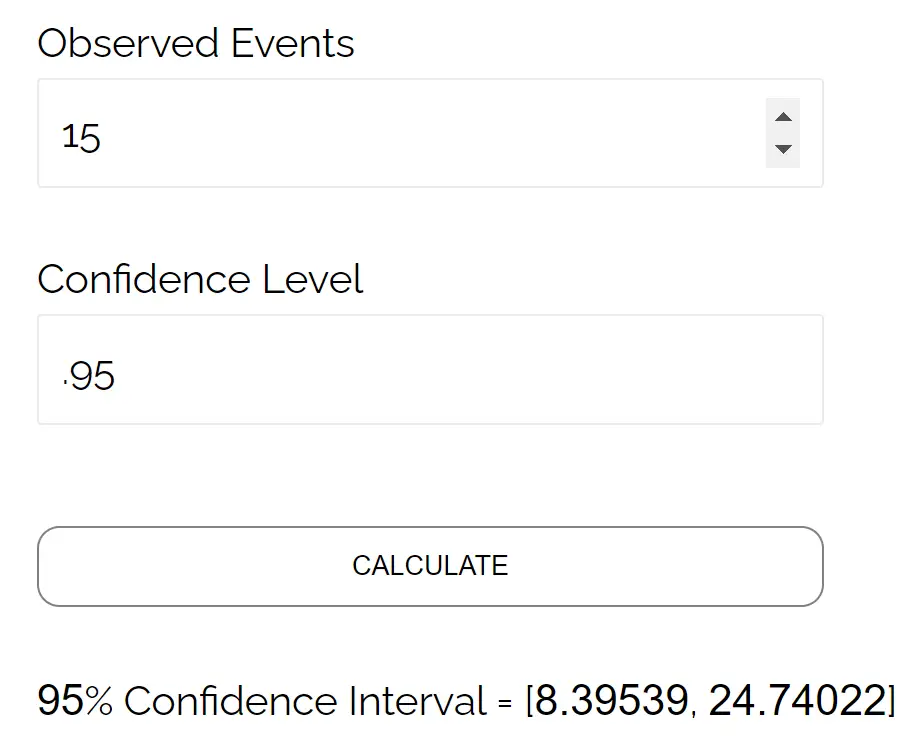
请注意，结果对应于我们手动计算的置信区间。