统计学中的贝塔水平是什么？ （定义&#038；示例）

在统计学中，我们使用假设检验来确定有关总体参数的假设是否正确。

假设检验总是有以下两个假设：

原假设 (H ₀ )：样本数据与总体参数的主导信念一致。

备择假设 ( _HA )：样本数据表明原假设中所述的假设不正确。换句话说，非随机原因会影响数据。

每当我们进行假设检验时，总是有四种可能的结果：

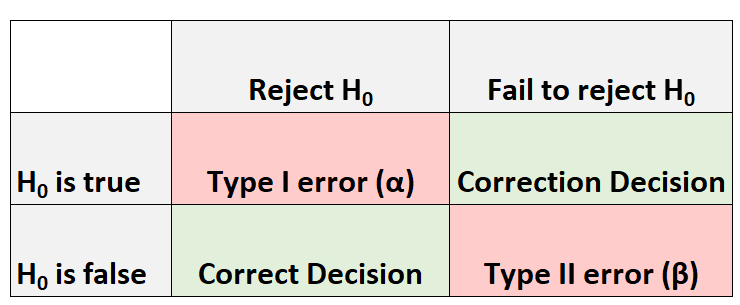
我们可能会犯两种类型的错误：

• 第一类错误：当零假设实际上为真时，我们拒绝它。犯这种错误的概率用α表示。
• 第二类错误：当原假设实际上是错误的时，我们未能拒绝它。犯这种错误的概率记为β 。

阿尔法与贝塔的关系

理想情况下，研究人员希望犯第一类错误的概率和犯第二类错误的概率都很低。

然而，这两个概率之间存在折衷。如果我们降低 alpha 水平，我们可能会降低拒绝原假设实际上为真的概率，但这实际上会增加 beta 水平——当原假设错误时我们无法拒绝原假设的概率。

幂与贝塔值的关系

假设检验的功效是指当效果或差异实际存在时检测到效果或差异的概率。换句话说，它是正确拒绝错误的原假设的概率。

计算方法如下：

功率 = 1 – β

一般来说，研究人员希望测试的功效较高，以便如果存在影响或差异，测试就能够检测到它。

从上面的等式中，我们可以看到，提高测试功效的最佳方法是降低 Beta 级别。降低贝塔水平的最佳方法通常是增加样本量。

以下示例展示了如何计算假设检验的 beta 水平，并演示了为什么增加样本量可以降低 beta 水平。

示例 1：计算假设检验的 Beta

假设研究人员想要测试工厂生产的小部件的平均重量是否低于 500 盎司。我们知道重量的标准差是 24 盎司，研究人员决定随机收集 40 个小部件样本。

当 α = 0.05 时，它将实现以下假设：

• H ₀ : µ = 500
• _HA ： μ<500

现在想象一下，生产的小部件的平均重量实际上是 490 盎司。换句话说，必须拒绝原假设。

我们可以使用以下步骤来计算贝塔水平——当原假设实际上应该被拒绝时却没有拒绝原假设的概率：

步骤1：找到无拒绝区域。

根据临界 Z 值计算器，α = 0.05 时的左临界值为-1.645 。

步骤 2：找到我们无法拒绝的最小样本。

检验统计量计算公式为 z = ( x – μ) / (s/ √n )

因此，我们可以求解该方程以获得样本均值：

• x = µ – z*(s/ √n )
• x = 500 – 1.645*(24/ √40 )
• x = 493.758

步骤 3：确定最小样本均值实际出现的概率。

我们可以如下计算这个概率：

• P(Z ≥ (493.758 – 490) / (24/√ 40 ))
• P(Z≥0.99)

根据普通CDF计算器，Z≥0.99的概率为0.1611 。

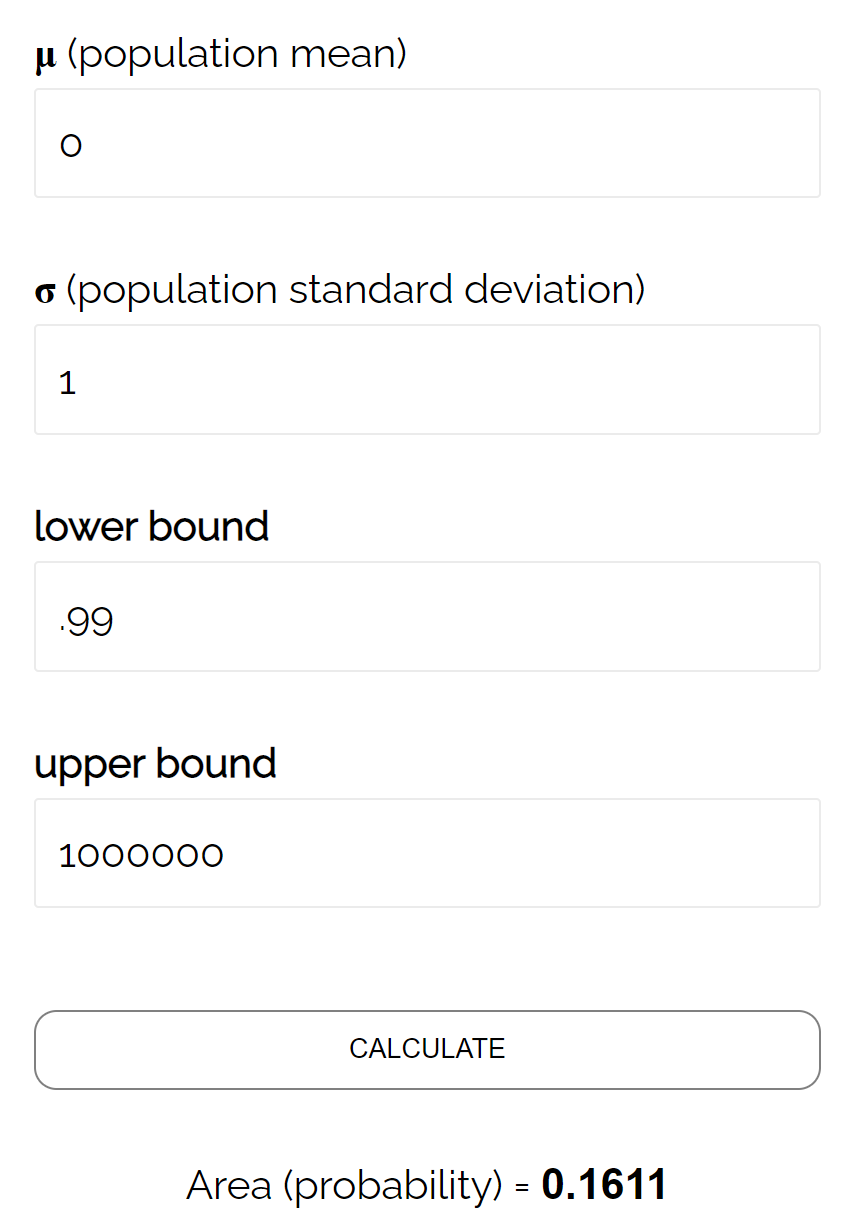
因此，该测试的 beta 水平为β = 0.1611。这意味着如果实际平均值为 490 盎司，则有 16.11% 的可能性无法检测到差异。

示例 2：计算具有较大样本量的测试的 Beta

现在假设研究人员执行完全相同的假设检验，但使用 n = 100 个小部件的样本。我们可以重复相同的三个步骤来计算此测试的 beta 级别：

步骤1：找到无拒绝区域。

根据临界 Z 值计算器，α = 0.05 时的左临界值为-1.645 。

步骤 2：找到我们无法拒绝的最小样本。

检验统计量计算公式为 z = ( x – μ) / (s/ √n )

因此，我们可以求解该方程以获得样本均值：

• x = µ – z*(s/ √n )
• x = 500 – 1.645*(24/√ 100 )
• x = 496.05

步骤 3：确定最小样本均值实际出现的概率。

我们可以如下计算这个概率：

• P(Z≥(496.05 – 490)/(24/ √100 ))
• P(Z≥2.52)

根据普通CDF计算器，Z≥2.52的概率为0.0059。

因此，该测试的 Beta 水平为β = 0.0059。这意味着如果实际平均值为 490 盎司，则只有 0.59% 的可能性无法检测到差异。

请注意，只需将样本量从 40 增加到 100，研究人员就能将 beta 水平从 0.1611 降低到 0.0059。

奖励：使用此 II 型误差计算器自动计算测试的 Beta 级别。

其他资源

假设检验简介
如何编写原假设（5 个示例）
P值和统计显着性的解释