留一交叉验证 (loocv) 快速简介
为了评估模型在数据集上的性能,我们需要衡量模型做出的预测与观察到的数据的匹配程度。
衡量这一点的最常见方法是使用均方误差 (MSE),其计算公式如下:
MSE = (1/n)*Σ(y i – f(x i )) 2
金子:
- n:观察总数
- y i :第 i 个观测值的响应值
- f( xi ):第 i个观测值的预测响应值
模型预测与观测值越接近,MSE 就越低。
在实践中,我们使用以下过程来计算给定模型的 MSE:
1.将数据集分为训练集和测试集。
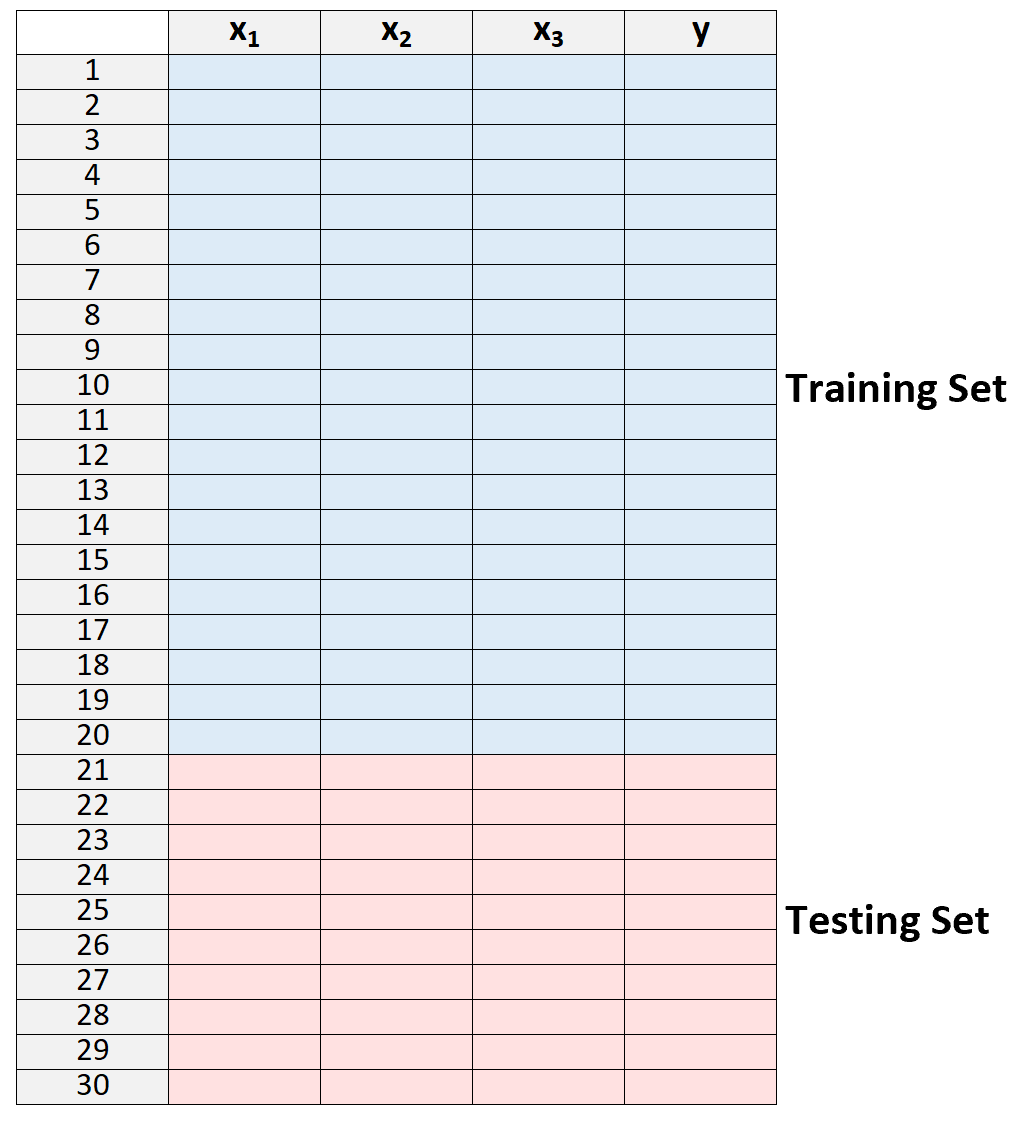
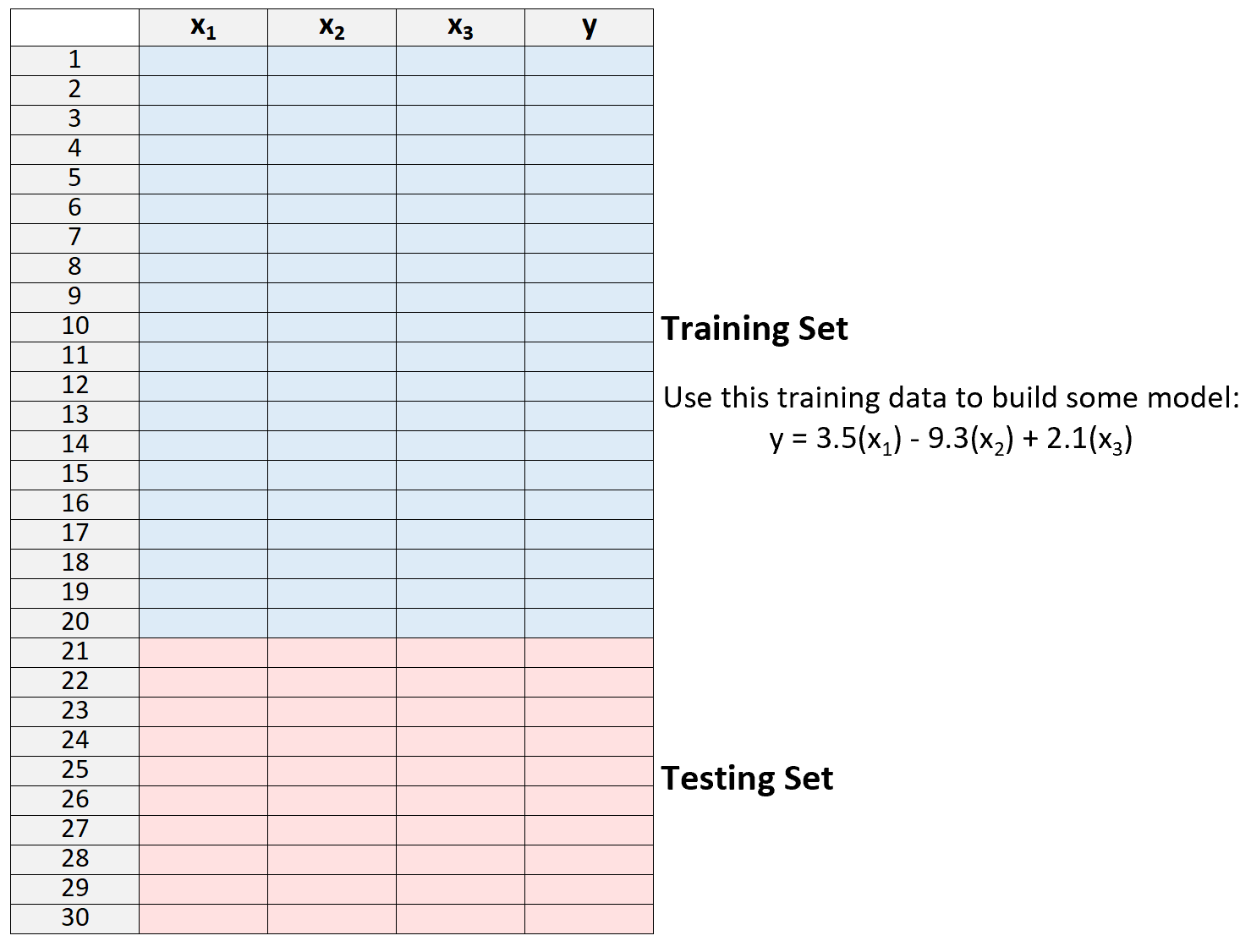
2.仅使用训练集中的数据创建模型。
3.使用模型对测试集进行预测并测量 MSE——这称为测试 MSE 。 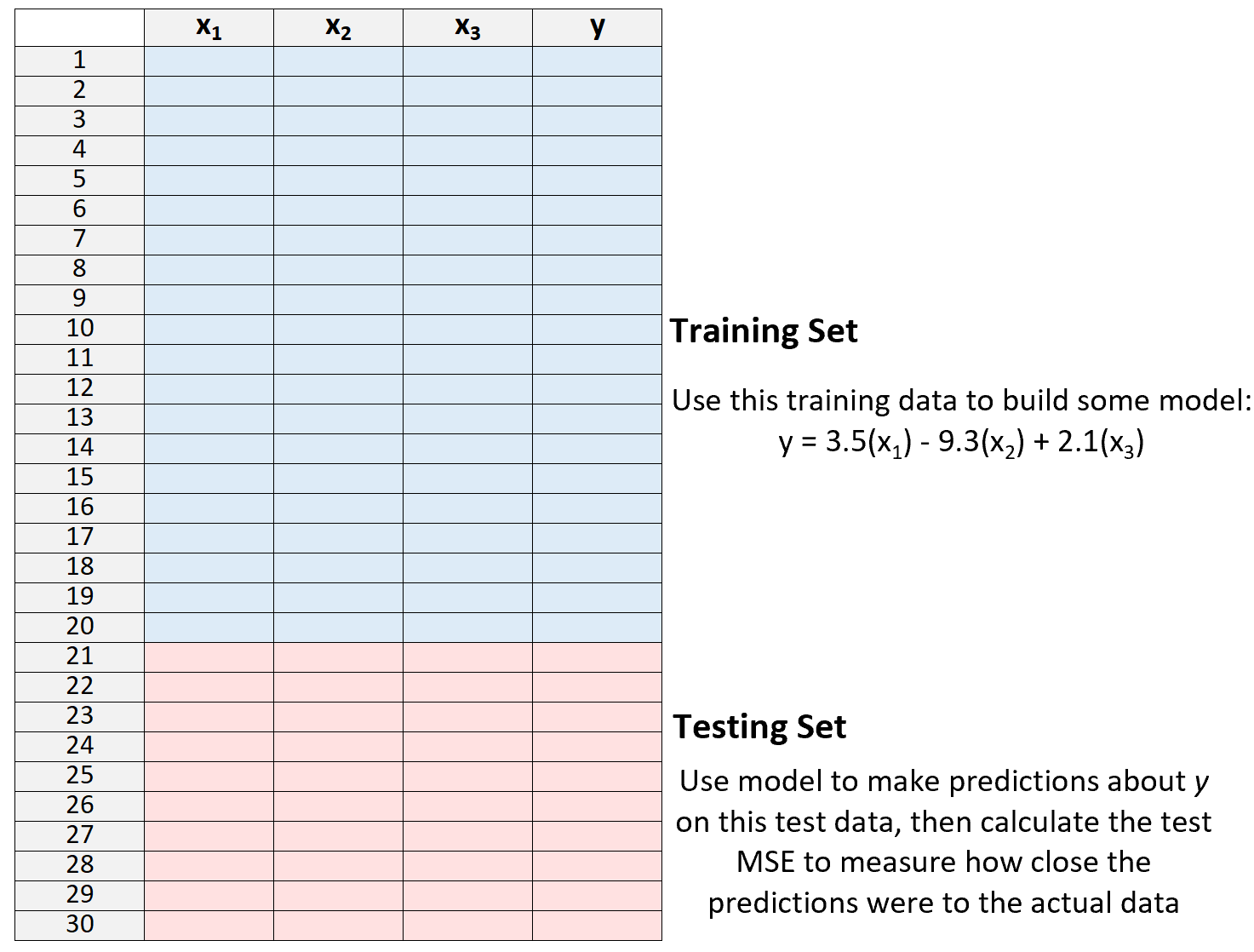
MSE 测试让我们了解模型在以前从未见过的数据(即尚未用于“训练”模型的数据)上的表现如何。
然而,使用单个测试集的缺点是 MSE 测试可能会根据训练和测试集中使用的观察结果而发生显着变化。
如果我们对训练集和测试集使用不同的观察集,我们的测试 MSE 可能会变得更大或更小。
避免此问题的一种方法是每次使用不同的训练和测试集多次拟合模型,然后将测试 MSE 计算为所有测试 MSE 的平均值。
这种通用方法称为交叉验证,其特定形式称为留一交叉验证。
留一交叉验证
留一法交叉验证使用以下方法来评估模型:
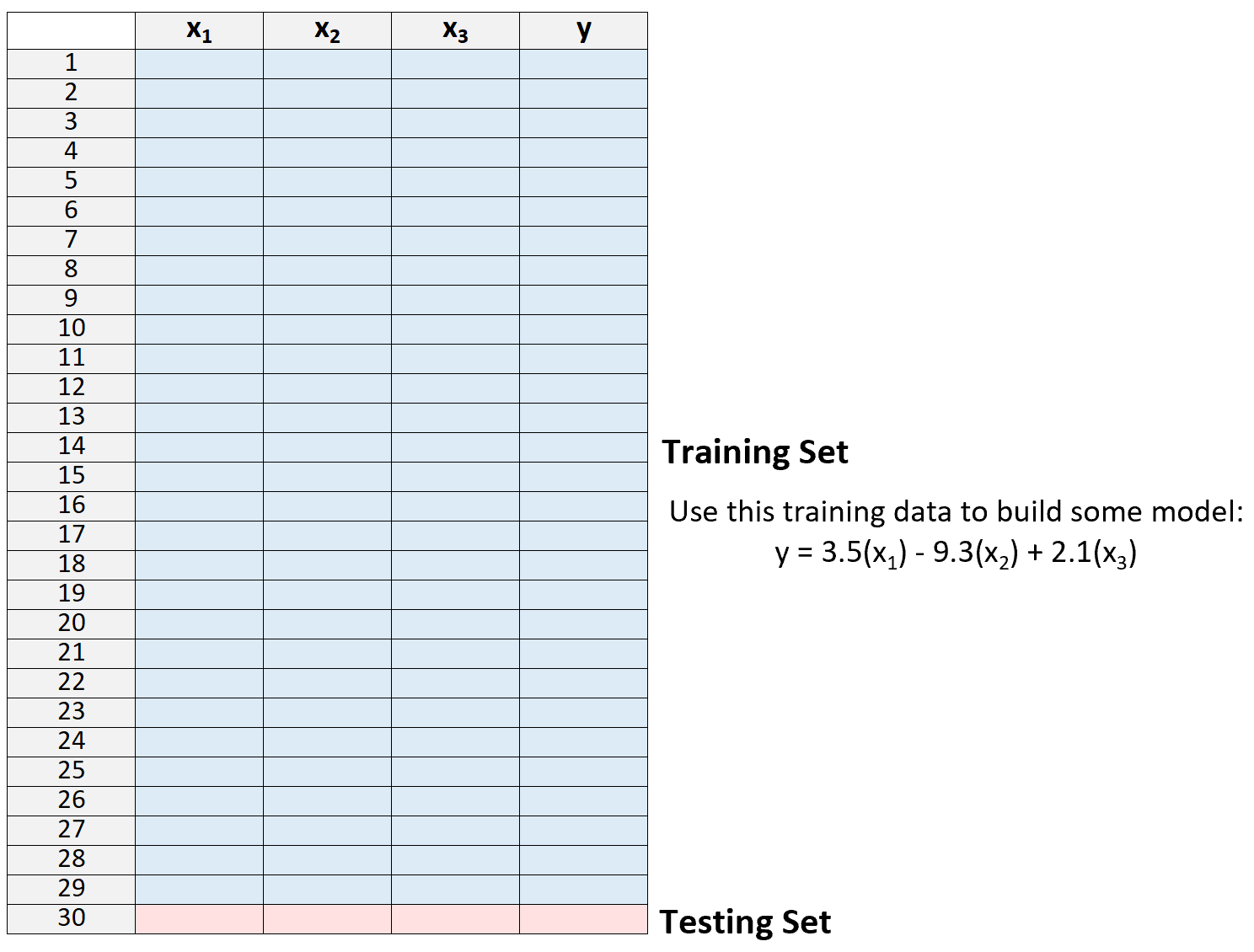
1.将数据集拆分为训练集和测试集,使用除一个观测值之外的所有观测值作为训练集的一部分:
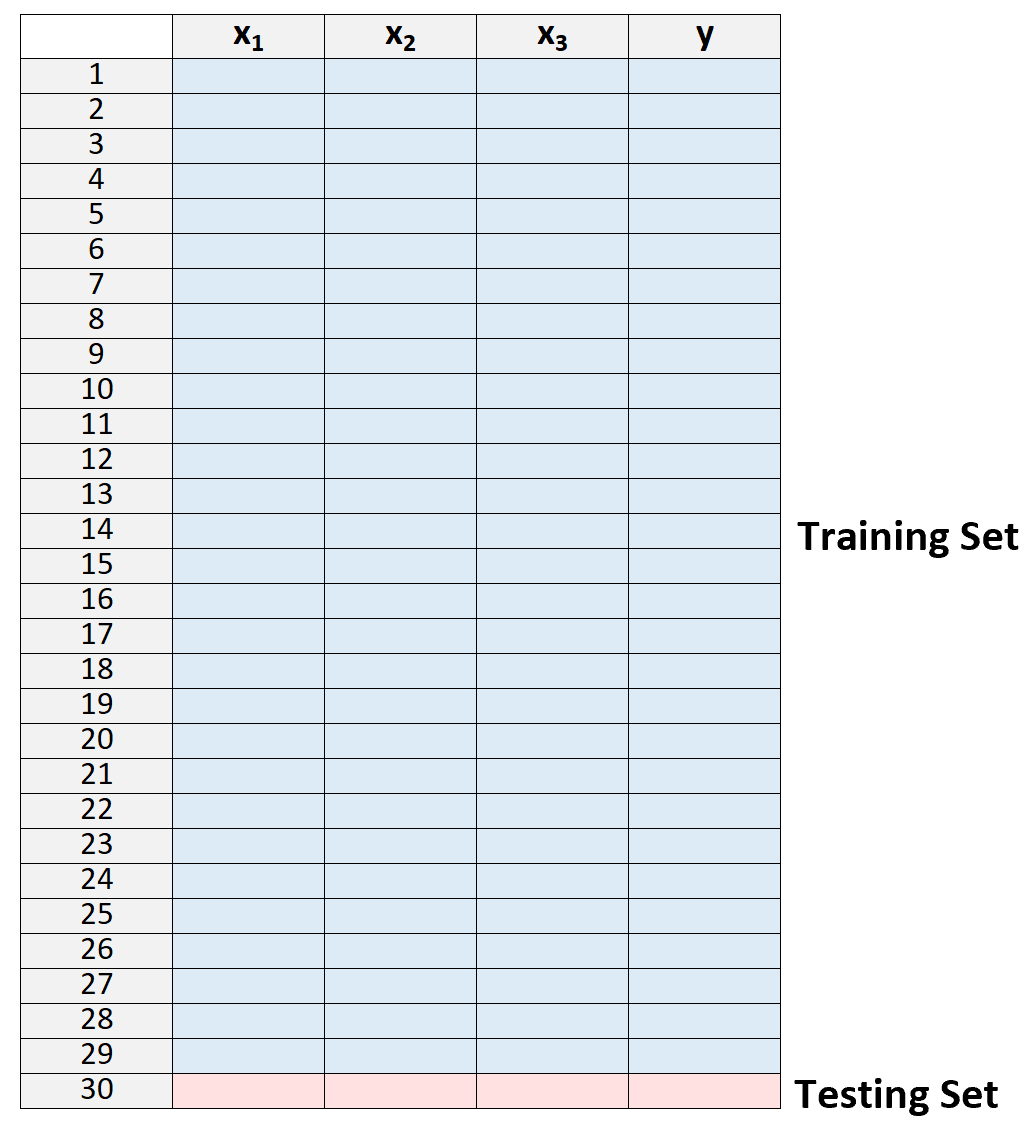
请注意,我们只在训练集“外部”留下一个观察结果。这就是该方法被称为“留一法”交叉验证的原因。
2.仅使用训练集中的数据创建模型。
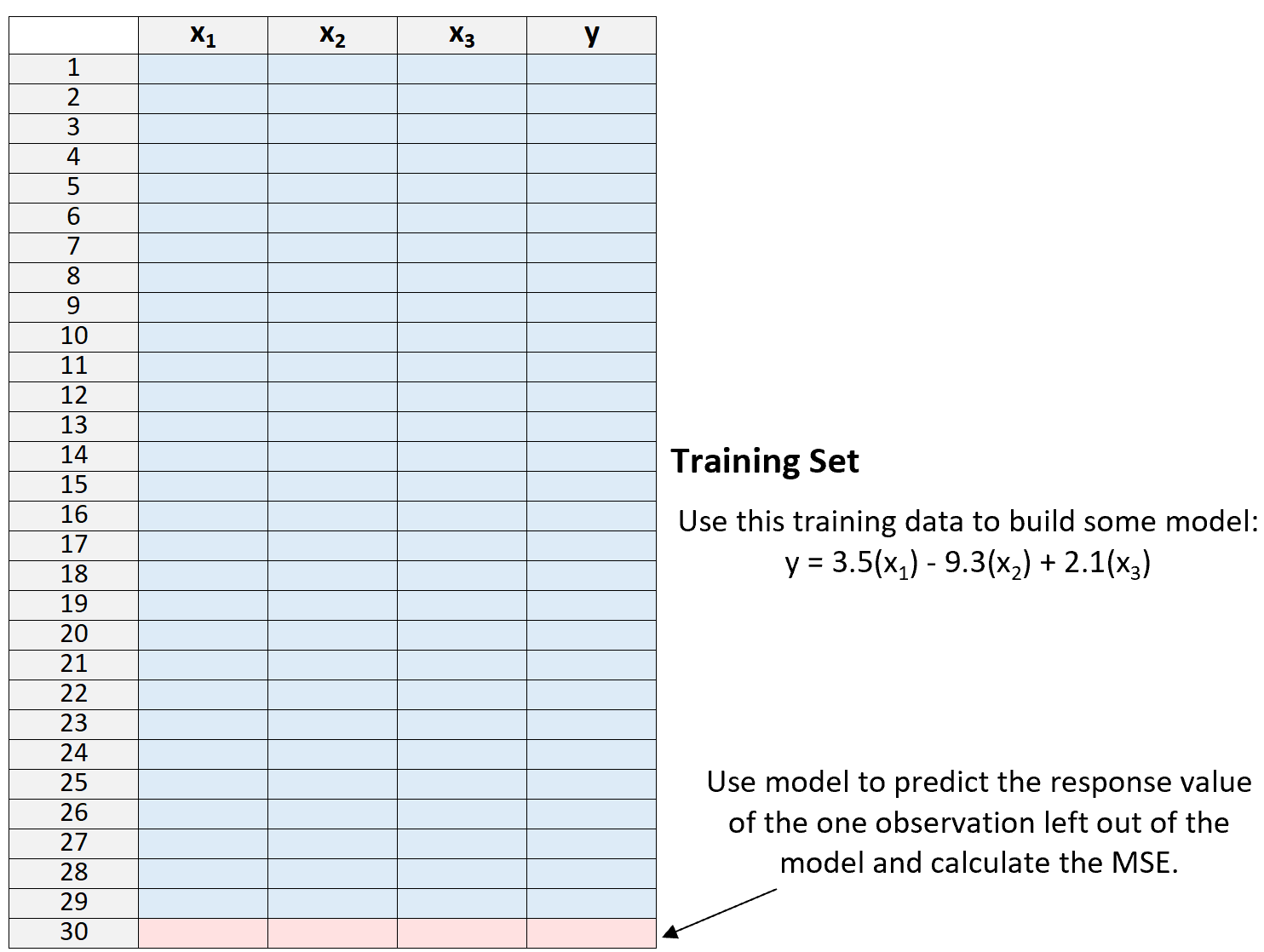
3.使用模型预测模型中排除的单个观测值的响应值并计算 MSE。
4.重复该过程n次。
最后,我们重复这个过程n次(其中n是数据集中的观察总数),每次从训练集中留下不同的观察结果。
然后我们将测试 MSE 计算为所有测试 MSE 的平均值:
MSE 检验 = (1/n)*ΣMSE i
金子:
- n:数据集中的观测总数
- MSEi:第i个模型拟合期间的MSE检验。
LOOCV的优点和缺点
留一交叉验证具有以下优点:
- 与使用单个测试集相比,它提供的 MSE 测试偏差要小得多,因为我们反复将模型拟合到包含n-1 个观测值的数据集。
- 与使用单个测试集相比,它往往不会高估测试的 MSE。
然而,不干涉交叉验证有以下缺点:
- 当n很大时,使用此过程可能需要很长时间。
- 如果模型特别复杂并且需要很长时间才能拟合数据集,则也可能非常耗时。
- 这在计算上可能是昂贵的。
幸运的是,现代计算在大多数领域已经变得非常高效,以至于 LOOCV 是一种比许多年前更合理的方法。
请注意,LOOCV 也可用于回归和分类上下文。对于回归问题,它将 MSE 检验计算为预测与观测值之间的均方根差,而在分类问题中,它将 MSE 检验计算为在模型的n次重复调整中正确分类的观测值的百分比。
如何在 R 和 Python 中运行 LOOCV
以下教程提供了有关如何在 R 和 Python 中为给定模型运行 LOOCV 的分步示例: