皮尔逊相关性的五个假设
皮尔逊相关系数（也称为“乘积矩相关系数”）衡量两个变量之间的线性关联。
它始终采用 -1 和 1 之间的值，其中：
- -1 表示两个变量之间完全负线性相关
- 0 表示两个变量之间不存在线性相关
- 1 表示两个变量之间存在完全正线性相关
然而，在计算两个变量之间的皮尔逊相关系数之前，我们必须确保满足五个假设：
1. 测量水平：两个变量都应在区间或比率水平上测量。
2.线性关系：两个变量之间必须存在线性关系。
3. 正态性：两个变量应近似呈正态分布。
4. 相关对：数据集中的每个观测值都必须有一对值。
5. 无异常值：数据集中不应存在极端异常值。
在本文中，我们对每个假设以及如何确定假设是否满足进行了解释。
假设1：测量水平
要计算两个变量之间的皮尔逊相关系数，必须在区间或比率水平上测量两个变量。
下图简要说明了可以测量变量的四个级别：
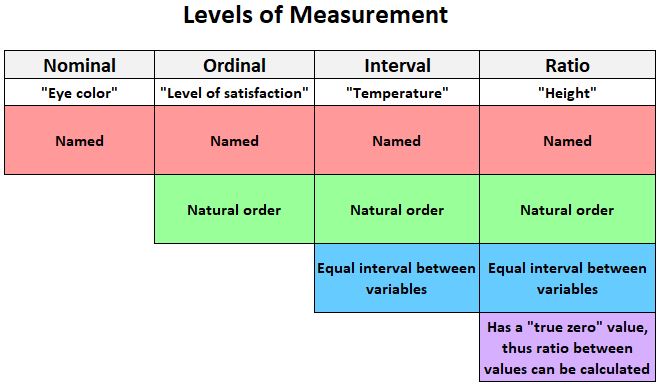
以下是可以在区间尺度上测量的变量的一些示例：
- 温度：以华氏度或摄氏度为单位测量
- 信用评分：从 300 到 850
- SAT 成绩： 400 至 1,600 分
以下是一些可以在比率尺度上测量的变量的示例：
- 高度：以厘米、英寸、英尺等为单位进行测量。
- 重量：以公斤、磅等计量单位。
- 长度：以厘米、英寸、英尺等为单位测量。
如果变量是按顺序测量的，那么您需要计算它们之间的Spearman 相关系数。
相关：测量级别：名义、序数、间隔和比率
假设2：线性关系
要计算两个变量之间的皮尔逊相关系数，两个变量之间必须存在线性关系。
检验这一假设的最简单方法是简单地创建两个变量的散点图。如果图上的点近似呈直线，则存在线性关系：
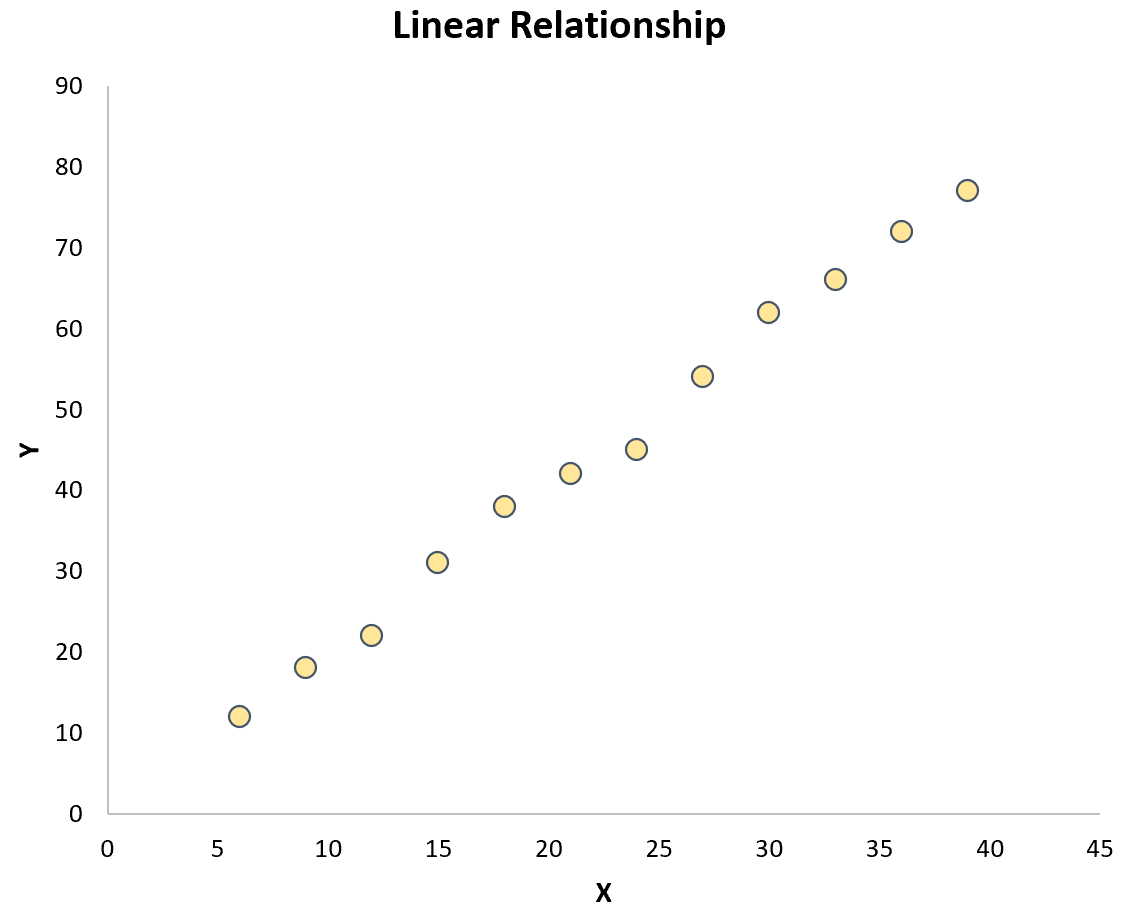
但是，如果点随机分散在图中或具有某种其他类型的关系（例如二次关系），则变量之间不存在线性关系：
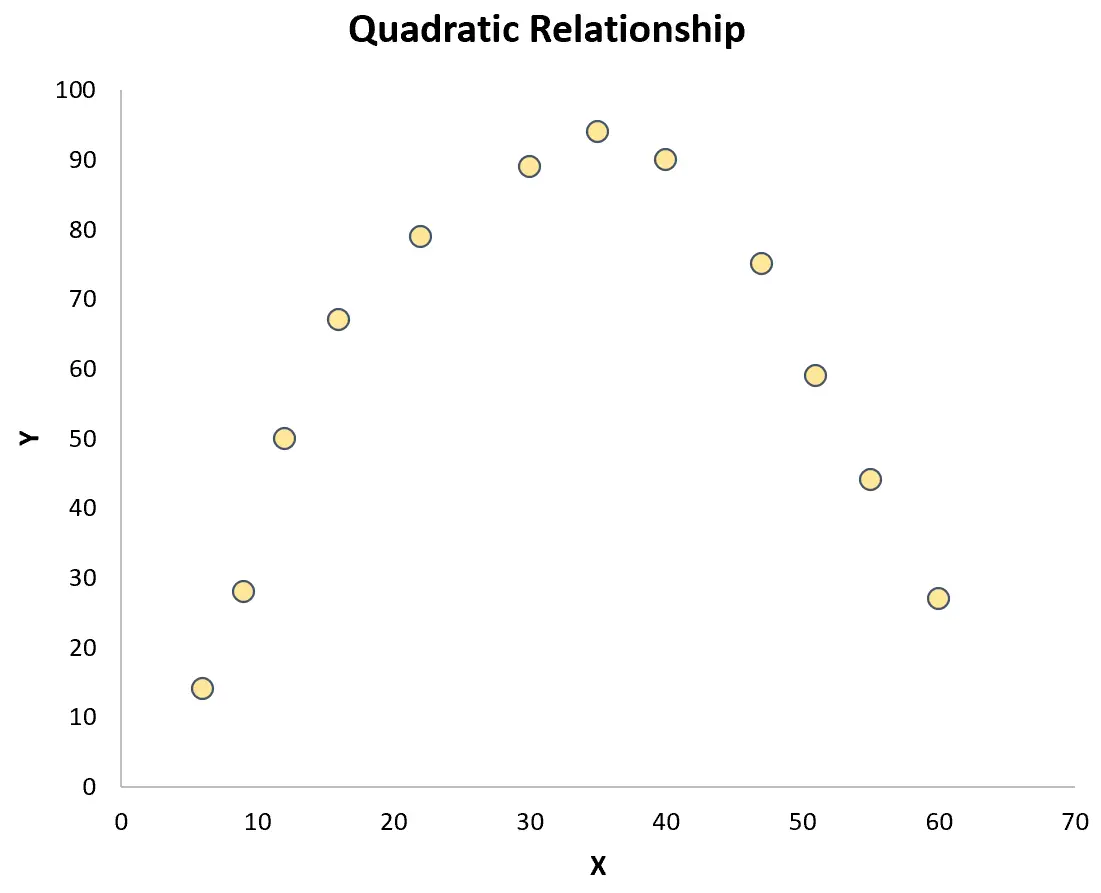
在这种情况下，皮尔逊相关系数将无法充分捕捉变量之间的关系。
假设3：正态性
Pearson 相关系数还假设两个变量近似呈正态分布。
您可以通过为每个变量创建直方图或 QQ 图来直观地验证此假设。
1. 直方图
如果数据集的直方图大致呈钟形，则该数据很可能呈正态分布。
2.QQ乐园
QQ 图是“分位数-分位数”的缩写，是一种沿 x 轴显示理论分位数（即数据服从正态分布时的位置）和沿 y 轴显示样本分位数的图。 （即您的数据实际所在的位置）。
如果数据值遵循形成 45 度角的大致直线，则假定数据呈正态分布。
您还可以执行正式的统计测试来确定变量是否呈正态分布。
如果检验的p 值低于一定的显着性水平（例如 α = 0.05），则您有足够的证据表明数据不呈正态分布。
常用来检验正态性的统计检验有以下三种：
1. 雅克-贝拉测试
2. 夏皮罗-威尔克检验
3. 柯尔莫哥洛夫-斯米尔诺夫检验
假设 4：相关对
皮尔逊相关系数还假设数据集中的每个观测值都必须有一对值。
这个假设很容易验证。例如，如果您要计算体重和身高之间的相关性，只需验证数据集中的每个观测值是否都有体重测量值和身高测量值。
假设 5：没有异常值
皮尔逊相关系数还假设数据集中不存在极端异常值，因为异常值强烈影响相关系数的计算。
为了说明这一点，请考虑以下数据集：
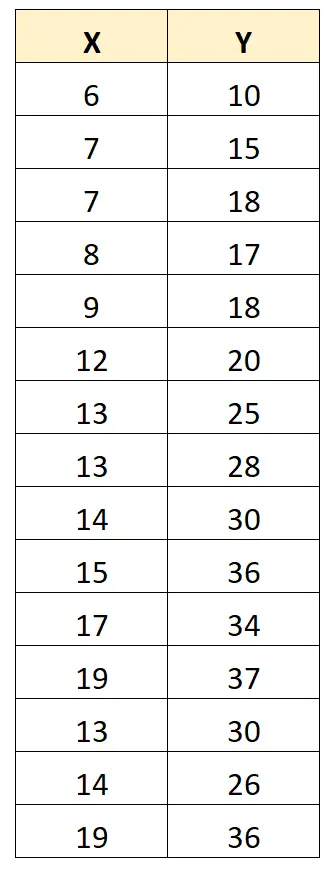
X 和 Y 之间的 Pearson 相关系数为0.949 。
但是，假设数据集中有一个异常值：
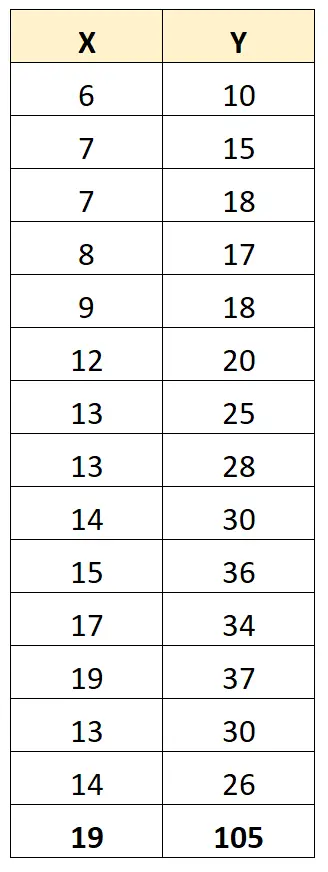
X 和 Y 之间的 Pearson 相关系数现在为0.711 。
异常值会显着改变两个变量之间的皮尔逊相关系数。在这种情况下，从数据集中删除异常值可能是有意义的。
其他资源
以下教程提供有关 Pearson 相关性的更多信息：
关于作者
本杰明·安德森博
大家好，我是本杰明，一位退休的统计学教授，后来成为 Statorials 的热心教师。 凭借在统计领域的丰富经验和专业知识，我渴望分享我的知识，通过 Statorials 增强学生的能力。了解更多