如何估计任何直方图的标准差
直方图提供了一种可视化数据集中值分布的有用方法。
直方图的 x 轴显示数据值组,y 轴告诉我们数据集中每组有多少个观测值。

由于直方图将观测值放入箱中,因此无法计算直方图表示的数据集的精确标准差,但可以估计标准差。
以下示例展示了如何执行此操作。
如何估计直方图的标准差
为了估计直方图的标准差,您必须首先估计平均值。
我们可以使用以下公式来估计平均值:
平均值: Σmin i / N
金子:
- mi : 第i个bin 的中间
- n i :第 i个bin 的频率
- N:总样本量
例如,假设我们有以下直方图:

以下是估计该直方图平均值的方法:
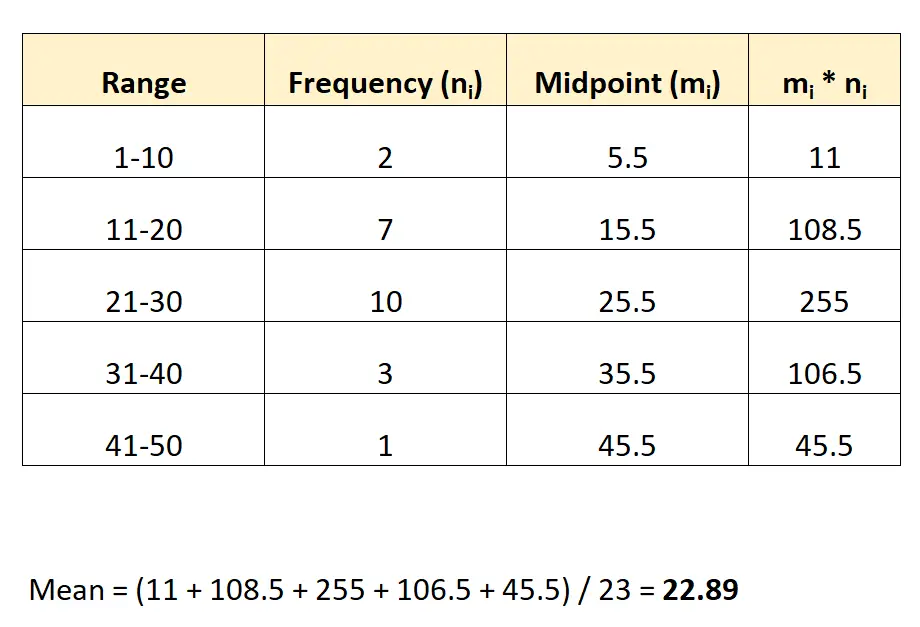
我们估计平均值为22.89 。
注:每组的中点可以通过取范围下限值和上限值的平均值来找到。例如,第一组的中点计算如下:(1+10)/2=5.5。
现在我们已经有了平均值的估计,我们可以使用以下公式来估计标准差:
标准差: √Σn i (m i -μ) 2 / (N-1)
金子:
- n i :第 i个bin 的频率
- mi : 第i个bin 的中间
- μ :平均值
- N:总样本量
以下是我们如何将此公式应用于我们的数据集:
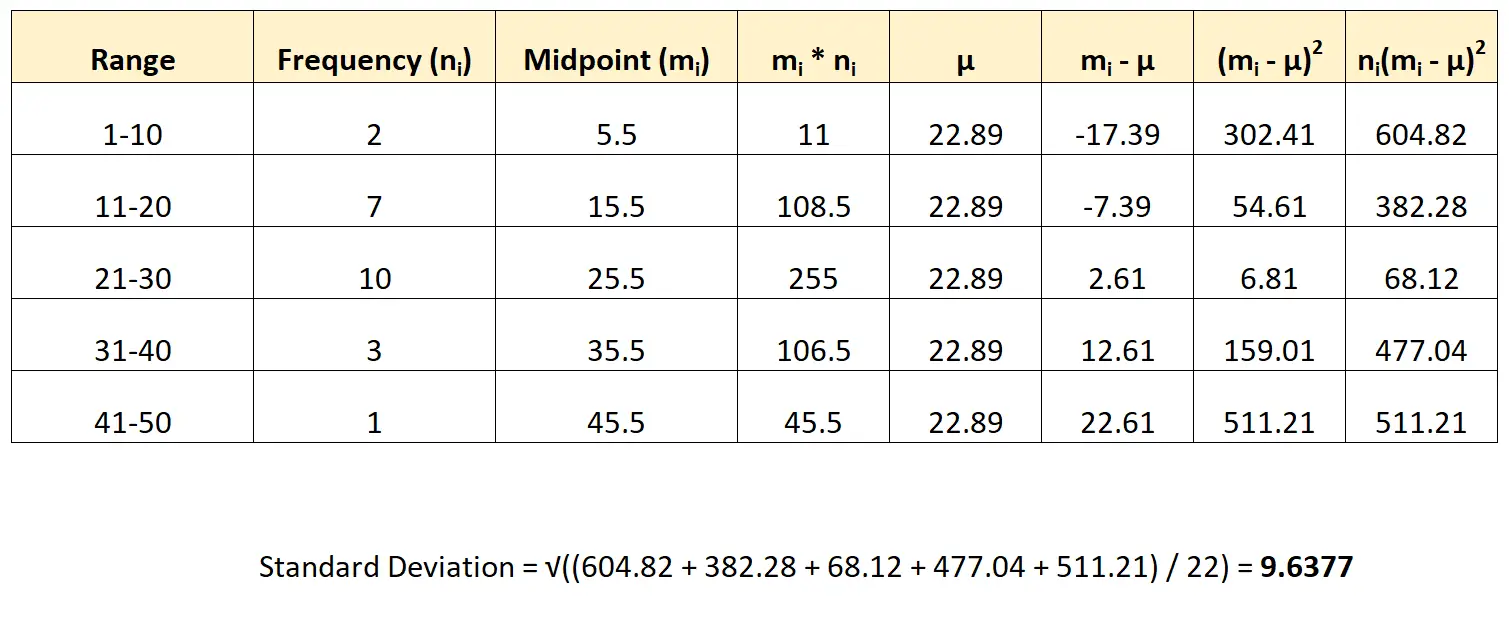 我们估计数据集的标准差为9.6377 。
我们估计数据集的标准差为9.6377 。
尽管不能保证它与数据集的标准差完全匹配(因为我们不知道数据集的原始数据值),但它代表了我们对标准差的最佳估计。
其他资源
以下教程说明如何执行与分组数据相关的其他常见任务: