相互包容或相互排斥的事件

如果两个事件不能同时发生，则它们是互斥的。

例如，假设事件A是骰子落在偶数上的事件，事件B是骰子落在奇数上的事件。

我们将事件的样本空间定义如下：

• A = {2, 4, 6}
• B = {1, 3, 5}

请注意，两个采样空间之间没有重叠。因此事件 A 和 B 是互斥的，因为它们不能同时发生。骰子落到的数字不能同时是偶数和奇数。

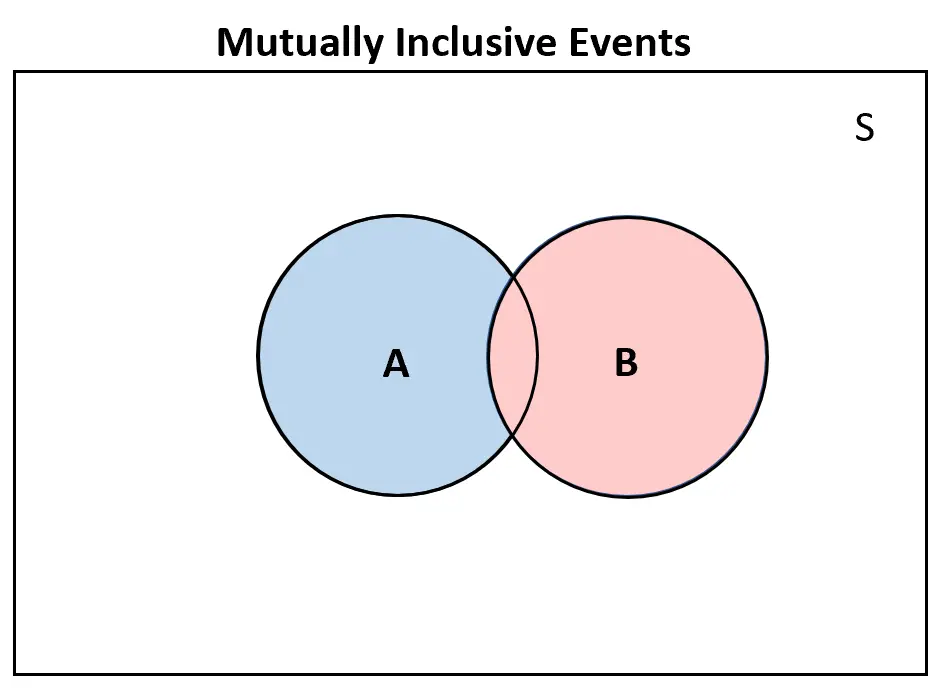
相反，如果两个事件可以同时发生，则它们是相互包含的。

例如，设事件 C 为骰子落在偶数上的事件，设事件 D 为骰子落在大于 3 的数字上的事件。

我们将事件的样本空间定义如下：

• C = {2, 4, 6}
• d = {4, 5, 6}

请注意，两个采样空间之间存在重叠。因此，事件 C 和 D 都是相互包含的，因为它们可以同时发生。骰子有可能落在大于 3 的偶数上。

事件概率

如果两个事件是互斥的，那么它们同时发生的概率为零。

例如，考虑上面事件 A 和 B 的两个示例空间：

• A = {2, 4, 6}
• B = {1, 3, 5}

由于样本空间没有重叠，我们可以说 P(A 和 B) = 0 。

但如果两个事件是相互包含的，那么它们同时发生的概率将是大于零的数字。

例如，考虑之前事件 C 和 D 的两个示例空间：

• C = {2, 4, 6}
• d = {4, 5, 6}

由于骰子可能落在 6 个可能的数字上，其中两个数字（4 和 6）同时属于事件 C 和 D，因此我们将 P(C 和 D) 计算为 2/6 或1/3 。

查看相互包容和相互排斥的事件

我们经常使用维恩图来可视化与事件相关的概率。

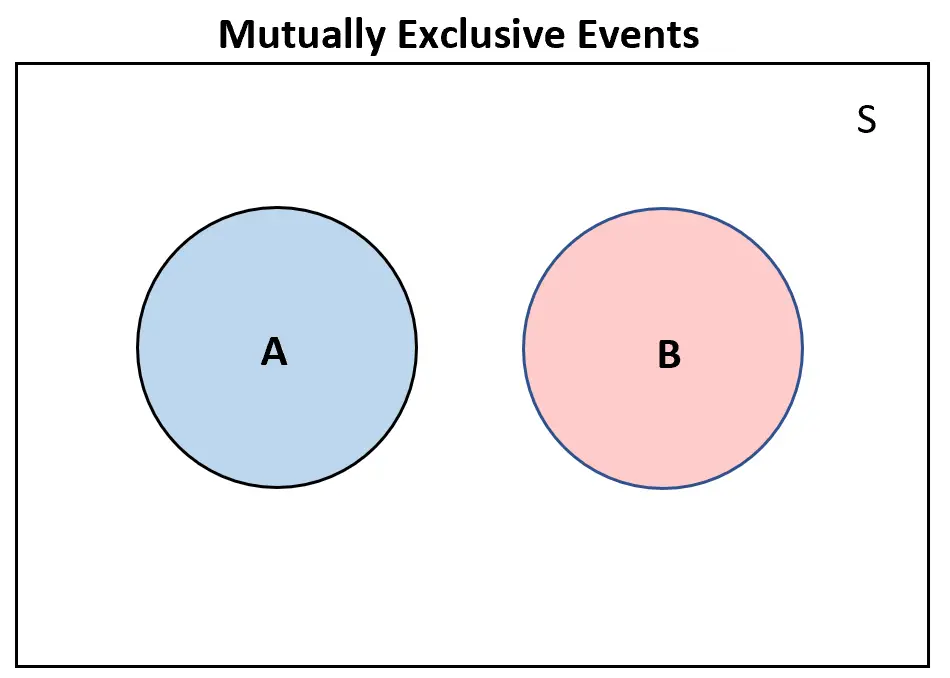
如果两个事件互斥，它们在维恩图中根本不会重叠：

相反，如果两个事件是相互包含的，则维恩图中至少会有一些重叠：

其他资源

理论概率简介
乘法的一般规则
什么是不相交事件？