相关与回归：有什么区别？

相关性和回归是两个相关但不完全相同的统计术语。

在本教程中，我们将简要解释这两个术语，并解释它们的相似点和不同点。

什么是相关性？

相关性衡量两个变量x和y之间的线性关联。它的值介于 -1 和 1 之间，其中：

• -1 表示两个变量之间完全负线性相关
• 0 表示两个变量之间不存在线性相关
• 1 表示两个变量之间存在完全正线性相关

例如，假设我们有以下包含两个变量的数据集：(1) 学习时间和 (2) 20 名不同学生收到的考试成绩：

如果我们创建一个学习时间与考试结果的散点图，它会是这样的：

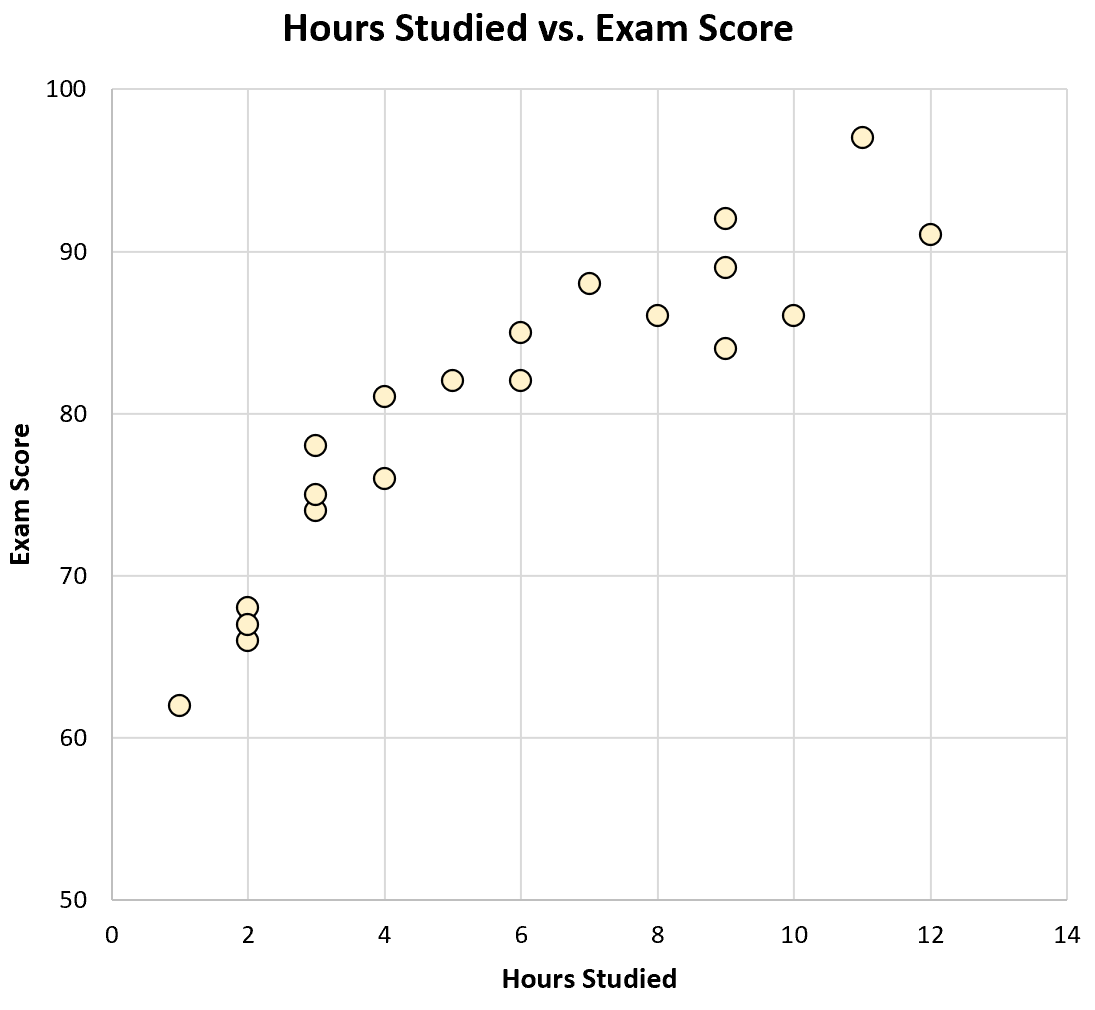
只要看一下图表，我们就可以看到学习更多的学生往往在考试中表现更好。也就是说，我们可以直观地看到两个变量之间存在正相关关系。

使用计算器，我们可以看到这两个变量之间的相关性为 r = 0.915 。该值接近 1，证实两个变量之间存在很强的正相关性。

什么是回归？

回归是我们可以用来理解改变变量x的值如何影响变量y的值的方法。

回归模型使用一个变量x作为预测变量，使用另一个变量y作为响应变量。然后，它找到最能描述两个变量之间关系的以下形式的方程：

ŷ = b ₀ + b ₁ x

金子：

• ŷ：响应变量的预测值
• b ₀ ：原点处的纵坐标（x等于0时y的值）
• b ₁ ：回归系数（x 增加一单位时 y 的平均增加）
• x：预测变量的值

例如，考虑我们之前的数据集：

使用线性回归计算器，我们发现以下方程最好地描述了这两个变量之间的关系：

预计考试成绩 = 65.47 + 2.58*（学习时间）

解释这个方程的方法是：

• 零学时学生的预计考试成绩是65.47 。
• 额外学习一小时的平均考试分数增加为2.58 。

我们还可以使用这个方程来预测学生根据学习小时数将获得的分数。

例如，学习 6 小时的学生应该获得80.95的成绩：

预计考试成绩 = 65.47 + 2.58*(6) = 80.95 。

我们还可以将该方程绘制为散点图上的一条线：

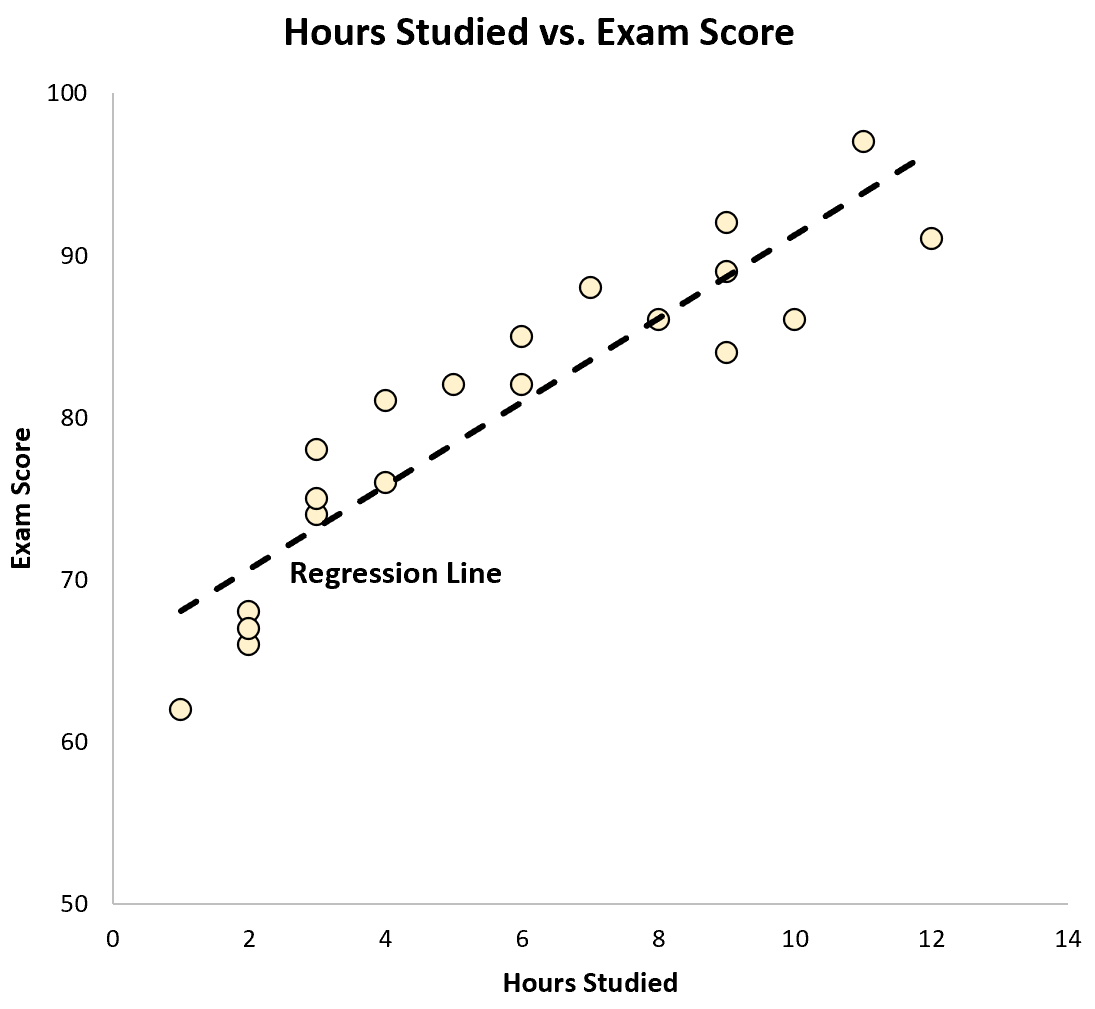
我们可以看到回归线很好地“拟合”了数据。

回想一下，这两个变量之间的相关性是 r = 0.915 。事实证明，我们可以对该值求平方并得到一个称为“r 平方”的数字，它描述了响应变量中可以由预测变量解释的方差的总比例。

在此示例中，r ² = 0.915 ² = 0.837 。这意味着 83.7% 的考试成绩差异可以通过学习时数来解释。

相关性与回归：相似点和差异

以下总结了相关性和回归之间的异同：

相似之处：

• 两者都量化两个变量之间关系的方向。
• 两者都量化两个变量之间关系的强度。

差异：

• 回归能够显示两个变量之间的因果关系。相关性并不能做到这一点。
• 回归能够使用方程根据另一个变量的值来预测一个变量的值。相关性并不能做到这一点。
• 回归使用方程来量化两个变量之间的关系。相关性使用单个数字。

其他资源

以下教程对本文所涵盖的主题进行了更深入的解释。

皮尔逊相关系数简介
简单线性回归简介
简单线性回归计算器
什么是好的 R 平方值？