相关矩阵

在本文中，您将了解什么是相关矩阵、其公式是什么以及如何解释相关矩阵。此外，您将能够看到相关矩阵解释的具体示例。

什么是相关矩阵？

相关矩阵是在位置i,j中包含变量i和j之间的相关系数的矩阵。

因此，相关矩阵是一个主对角线上填满 1 的方阵，第i行j列的元素由变量i和变量j之间的相关系数值组成。

因此相关矩阵的公式如下：

金子

是变量之间的相关系数

和

因此，为了找到数据集的相关矩阵，了解相关系数的计算方式至关重要。如果您不记得了，在以下链接中您将了解如何使用在线计算器进行计算：

相关系数的一个性质是变量的顺序与其计算无关，即相关系数

相当于

因此，相关矩阵是对称的。

为了使相关矩阵有意义，统计数据集必须具有两个以上变量。否则，确定单个相关系数就足够了，相关矩阵也有意义。

如何制作相关矩阵

给定相关矩阵的定义，让我们看看这种类型的统计矩阵是如何创建的：

1. 计算每对变量的相关系数。请注意，变量的顺序不会改变结果，因此只需为每对变量计算一次。
2. 创建一个与数据系列中变量数量相同维度的方阵。该矩阵将是相关矩阵。
3. 将 1 放入相关矩阵主对角线的每个元素中。
4. 将变量i , j的相关系数放在位置i , j和j , i处。
5. 创建相关矩阵后，剩下的就是解释其值。

请记住，仅仅运行相关矩阵是不够的，您还需要解释其值并理解它们的含义。以下部分解释如何解释相关矩阵。

相关矩阵的解释

为了正确解释相关矩阵，需要考虑到相关系数的值可以在 -1 到 +1 的范围内：

• r=-1 ：两个变量具有完美的负相关性，因此我们可以画一条负斜率的线，将所有点连接起来。
• -1<r<0 ：两个变量之间的相关性为负，因此当一个变量增加时另一个变量减少。该值越接近-1，变量负相关程度越高。
• r=0 ：两个变量之间的相关性很弱，实际上它们之间的线性关系为零。这并不意味着变量是独立的，因为它们可能具有非线性关系。
• 0<r<1 ：两个变量之间的相关性为正，值越接近+1，变量之间的相关性越强。在这种情况下，当另一个变量也增加时，一个变量的值往往会增加。
• r=1 ：两个变量具有完美的正相关性，即呈正线性关系。

因此，为了解释相关矩阵，有必要解释每个相关系数并比较不同的结果。

通过这种方式，您将能够看到哪些变量彼此最相关，哪些变量最重要，哪些变量彼此几乎没有关系等等。

相关矩阵示例

为了充分理解相关矩阵的组成以及如何解释它，在本节中我们将分析一个相关矩阵的示例：

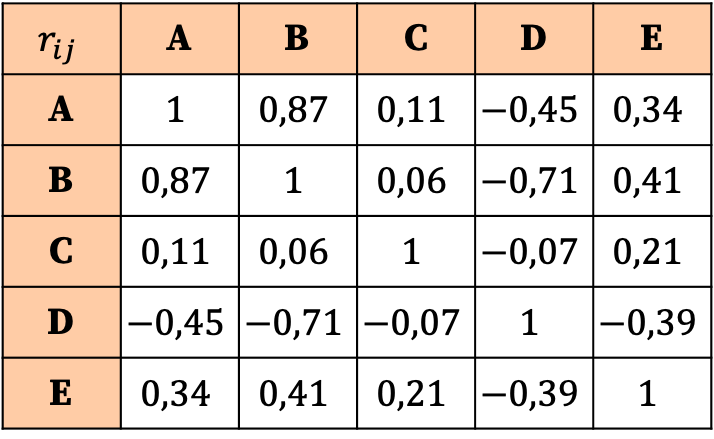
相关矩阵的解释基于系数的值。由此可见，相关性最强的是变量A和变量B之间的关系，因为它对应的系数最大（0.87）。

另一方面，变量 C 实际上与任何变量都没有相关性，因为它的所有系数都非常接近于零，因此非常低。因此，为了简化分析，我们甚至可以考虑从统计研究中删除这个变量。

类似地，变量D与其他变量的所有关系都是负相关，这意味着变量D与其他变量之间的相关性是反比的。这并不意味着该变量应该被消除，只是变量 D 是负相关的。

可以看到，相关矩阵对于汇总数据以及对数据集中不同变量之间的关系进行整体分析非常有用。