如何计算相对风险的置信区间

分析 2×2 表时通常会计算相对风险，该表采用以下格式：

相对风险告诉我们，与对照组中发生事件的可能性相比，治疗组中发生事件的可能性。

计算方法如下：

• 相对风险= [A/(A+B)] / [C/(C+D)]

然后，我们可以使用以下公式来计算相对风险 (RR) 的置信区间：

• CI 小于 95% ^{= eln(RR) – 1.96√ 1/a + 1/c – 1/(a+b) – 1/(c+d)}
• CI 大于 95% = ^{eln(RR) + 1.96√ 1/a + 1/c – 1/(a+b) – 1/(c+d)}

下面的例子展示了在实践中如何计算相对风险和相应的置信区间。

示例：计算相对风险的置信区间

假设篮球教练使用新的训练计划，看看与旧的训练计划相比，它是否增加了能够通过某种技能测试的球员数量。

教练招募 50 名球员使用每个程序。下表显示了通过和未通过技能测试的玩家数量（基于他们使用的程序）：

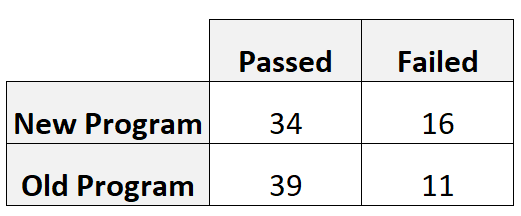
我们可以计算相对风险如下：

• 相对风险 = [A/(A+B)] / [C/(C+D)]
• 相对风险 = [34/(34+16)] / [39/(39+11)]
• 相对风险 = 0.8718

我们将此解释为，使用新程序的玩家通过测试的概率仅为使用旧程序的玩家通过测试的概率的 0.8718 倍。

换句话说，通过使用新程序，玩家通过测试的可能性实际上降低了。

然后我们可以使用以下公式来计算相对风险的 95% 置信区间：

• CI 小于 95% = ^{eln(.8718) – 1.96√ (1/34 + 1/39 – 1/(34+16) – 1/(39+11)} = 0.686
• CI 大于 95% = e ^{ln(.8718) + 1.96√ (1/34 + 1/39 + 1/(34+16) – 1/(39+11)} = 1.109

因此，相对风险的 95% 置信区间为[0.686, 1.109] 。

我们有 95% 的信心认为新旧培训计划之间的真实相对风险包含在这个区间内。

由于该置信区间包含值 1，因此不具有统计显着性。

当您考虑以下因素时，这应该是有意义的：

• 大于1的相对风险意味着玩家使用新程序通过测试的概率大于玩家使用旧程序通过测试的概率。
• 小于 1 的相对风险意味着玩家使用新程序通过测试的概率小于玩家使用旧程序通过测试的概率。

因此，由于相对风险的 95% 置信区间包含值 1，这意味着玩家使用新程序通过技能测试的概率可能会或可能不会大于同一玩家使用新程序通过测试的概率。新计划。旧程序。

其他资源

以下教程提供了有关优势比和相对风险的更多信息：

如何解释优势比
如何解释相对风险
如何在 Excel 中计算优势比和相对风险