如何求抛硬币中至少出现正面朝上的概率

对于给定的抛硬币，正面朝上的概率为 1/2 或 0.5。

要计算在一定次数的抛硬币中至少出现正面朝上的概率，可以使用以下公式：

P（至少一个头）= 1 – 0.5 ⁿ

金子：

• n ：反转总数

例如，假设我们抛硬币两次。

在这 3 次投掷中至少获得 1 个正面的概率为：

• P（至少一个头）= 1 – 0.5 ⁿ
• P（至少一个头）= 1 – 0.5 ³
• P（至少一个头）= 1 – 0.125
• P（至少一个头）= 0.875

如果我们列出抛硬币 2 次的所有可能结果，其中“T”代表正面，“H”代表反面，这个答案就有意义了：

• TT
• 总台
• THH
• THT
• 呵呵呵呵
• 虚拟现实开发
• 华泰
• 高温试验

请注意，8 种可能结果中，至少有 7 种出现正面 (H)，相当于 7/8 = 0.875 。

或者假设我们抛硬币 5 次。

在这 5 次投掷中至少获得 1 个正面的概率为：

• P（至少一个头）= 1 – 0.5 ⁿ
• P(至少一个头) = 1 – 0.5 ⁵
• P（至少一个头）= 1 – 0.25
• P(至少一个头) = 0.96875

下表显示了在抛掷不同次数的硬币时至少出现一个正面的概率：

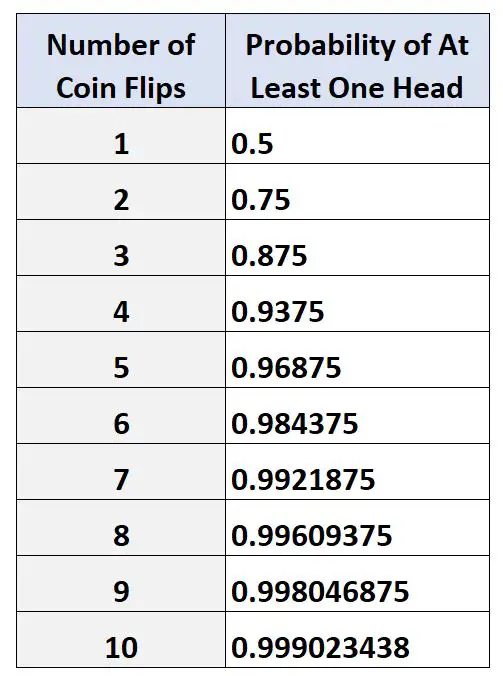
请注意，抛硬币的次数越多，获得至少一个正面的概率就越高。

考虑到如果我们继续多次抛硬币，最终看到正面出现的概率应该更高，这应该是有道理的。

其他资源

以下教程解释了如何执行其他常见的概率相关计算：

如何找到“至少一次”成功的概率
如何找到“至少两次”成功的概率
如何求A和B的概率
如何求 A 或 B 的概率