什么是 cochran's q 检验？ （定义&#038；示例）

Cochran’s Q 检验是一种统计检验，用于确定三个或更多组中“成功”的比例是否相等，其中每个组中出现相同的个体。

例如，我们可以使用 Cochran 的 Q 检验来确定在使用三种不同的学习技术时通过测试的学生比例是否相等。

执行 Cochran Q 检验的步骤

Cochran 的 Q 检验使用以下原假设和备择假设：

原假设 (H ₀ )：所有组中“成功”的比例相同

备择假设 ( _HA )：至少其中一组的“成功”比例不同

检验统计量计算如下：

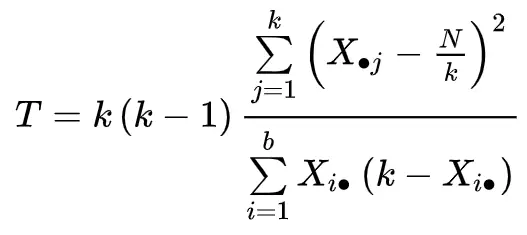
金子：

• k：治疗次数（或“组”）
• Xj：^{第 j 个}处理的列的总计
• b：块数
• 奚。 ：^{第 i 个}块的行总数
• N：总计

T检验统计量遵循自由度为k-1 的卡方分布。

如果与检验统计量相关的p 值低于一定的显着性水平（例如 α = 0.05），我们可以拒绝零假设并得出结论，我们有足够的证据表明“成功”的比例在至少其中一组。

示例：Cochran 的 Q 检验

假设研究人员想知道三种不同的学习技巧是否会导致学生成功率的比例不同。

为了测试这一点，她招募了 20 名学生，每人使用三种不同的学习技巧参加同等难度的考试。结果如下所示：

为了执行 Cochran 的 Q 检验，我们可以使用统计软件，因为手动执行可能很繁琐。

以下是我们可以用来创建此数据集并在 R 统计编程语言中执行 Cochran’s Q 检验的代码：

 #load DescTools package
library (DescTools)

#create dataset
df <- data.frame(student= rep (1:20, each = 3 ),
                 technique= rep (c('A', 'B', 'C'), times= 20 ),
                 outcome=c(1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1,
                           1, 1, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 1,
                           1, 0, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1,
                           1, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1))

#perform Cochran's Q test
CochranQTest(outcome ~ technique| student, data=df)

	Cochran's Q test

data: outcome and technique and student
Q = 0.33333, df = 2, p-value = 0.8465

从测试结果我们可以观察到以下几点：

• 检验统计量为0.333
• 相应的 p 值为0.8465

由于该 p 值不小于 0.05，因此我们无法拒绝原假设。

这意味着我们没有足够的证据表明学生使用的学习技巧会导致不同比例的成功率。