如何在 excel 中执行 kolmogorov-smirnov 检验

柯尔莫哥洛夫-斯米尔诺夫检验用于确定样本是否服从正态分布。

该检验被广泛使用，因为许多统计检验和程序都假设数据呈正态分布。

以下分步示例演示如何对 Excel 中的示例数据集执行 Kolmogorov-Smirnov 检验。

第 1 步：输入数据

我们首先输入样本大小为 n = 20 的数据集中的值：

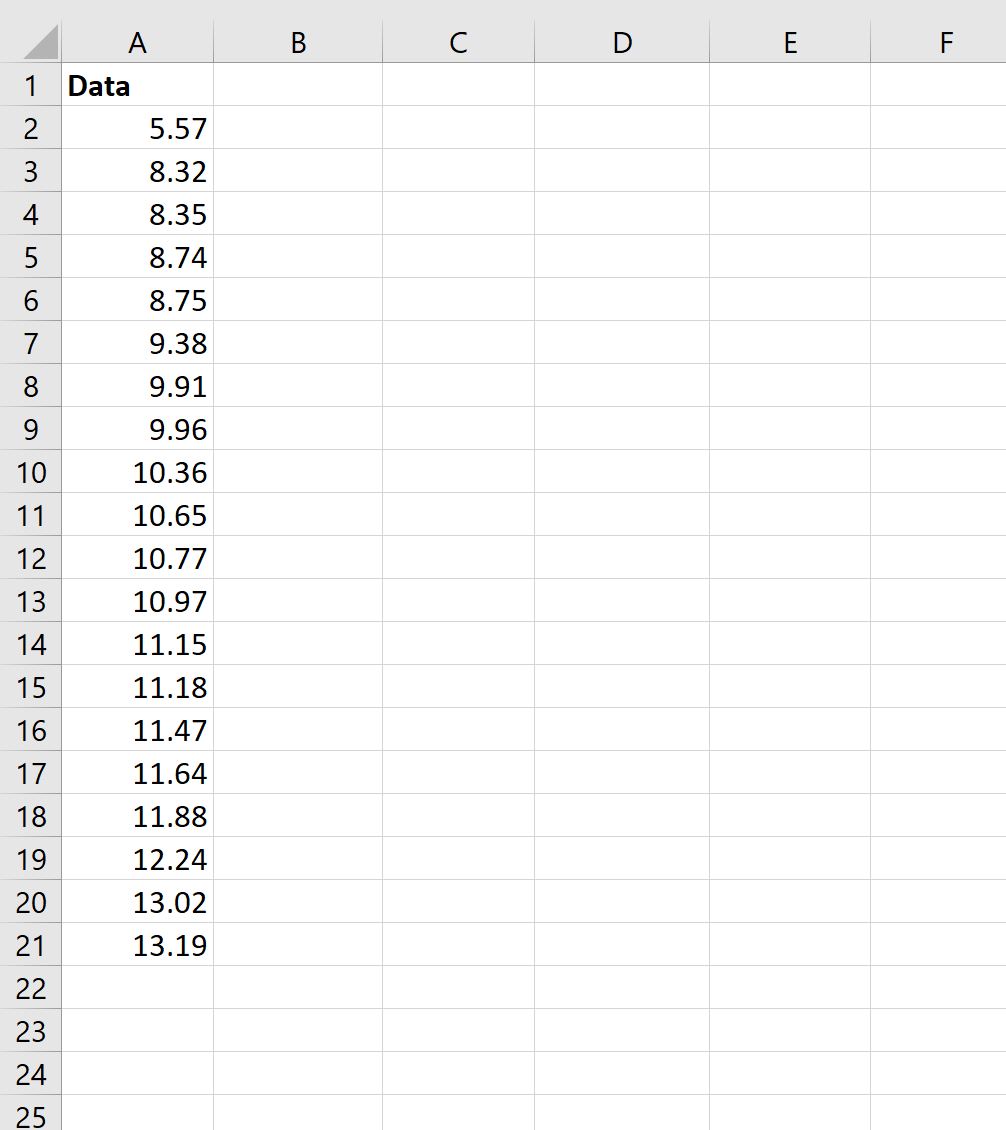
步骤 2：根据正态分布计算实际值和期望值

接下来，我们将计算正态分布的实际值与期望值：

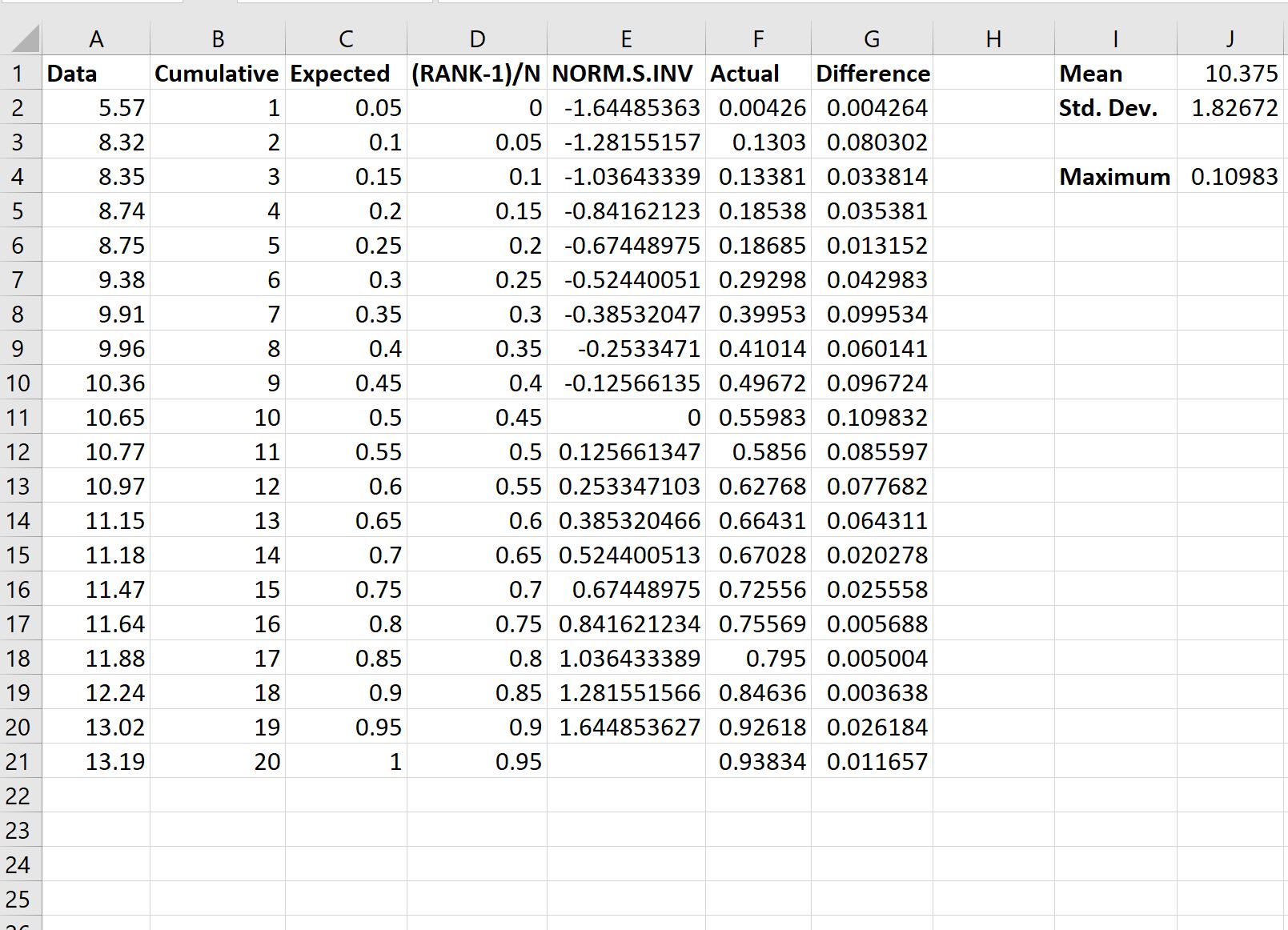
这是我们在不同单元格中使用的公式：

• B2 : =LINE() – 1
• C2 : = B2 /COUNT( $A$2:$A$21 )
• D2 : =( B2 -1)/COUNT( $A$2:$A$21 )
• E2 : =IF( C2 <1, NORM.S.INV( C2 ),”)
• F2 : =NORM.DIST( A2 , $J$1 , $J$2 , TRUE)
• G2 : =ABS( F2 – D2 )
• D1 : =平均值( A2:A21 )
• J2 : =ETDEV.S( A2:A21 )
• J4 : =MAX( G2:G21 )

第 3 步：解释结果

Kolmogorov-Smirnov 检验使用以下原假设和备择假设：

• H ₀ ：数据呈正态分布。
• H _A ：数据不呈正态分布。

为了确定是否应该拒绝原假设，我们需要参考输出中的最大值，结果为0.10983 。

这表示我们样本的实际值与正态分布的期望值之间的最大绝对差。

要确定这个最大值是否具有统计显着性，必须参考 Kolmogorov-Smirnov 临界值表并找到等于 n = 20 且 α = 0.05 的数字。

临界值为0.190 。

由于我们的最大值不大于该临界值，因此我们无法拒绝原假设。

这意味着我们可以假设我们的样本数据是正态分布的。

其他资源

以下教程解释了如何在 Excel 中执行其他常见统计测试：

如何在Excel中进行相关性测试
如何在 Excel 中执行 Durbin-Watson 检验
如何在 Excel 中执行 Jarque-Bera 检验
如何在 Excel 中执行 Levene 检验