如何在 python 中执行 box-cox 变换

Box-Cox 变换是将非正态分布的数据集变换为更正态分布的数据集的常用方法。

此方法背后的基本思想是使用以下公式找到 λ 值，使变换后的数据尽可能接近正态分布：

• y(λ) = (y ^λ – 1) / λ 如果 y ≠ 0
• y(λ) = log(y) 如果 y = 0

我们可以使用scipy.stats.boxcox()函数在 Python 中执行 box-cox 转换。

下面的例子展示了如何在实际中使用这个功能。

示例：Python 中的 Box-Cox 变换

假设我们根据指数分布生成一组随机的 1000 个值：

 #load necessary packages
import numpy as np 
from scipy. stats import boxcox 
import seaborn as sns 

#make this example reproducible
n.p. random . seeds (0)

#generate dataset
data = np. random . exponential (size= 1000 )

#plot the distribution of data values
sns. distplot (data, hist= False , kde= True ) 

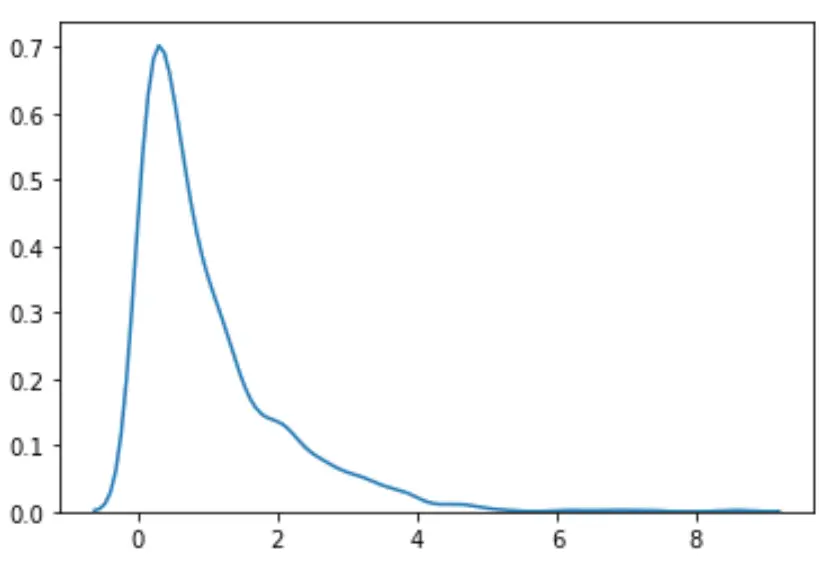
我们可以看到分布看起来不正常。

我们可以使用boxcox()函数来找到产生更正态分布的 lambda 最佳值：

 #perform Box-Cox transformation on original data
transformed_data, best_lambda = boxcox(data) 

#plot the distribution of the transformed data values
sns. distplot (transformed_data, hist= False , kde= True ) 

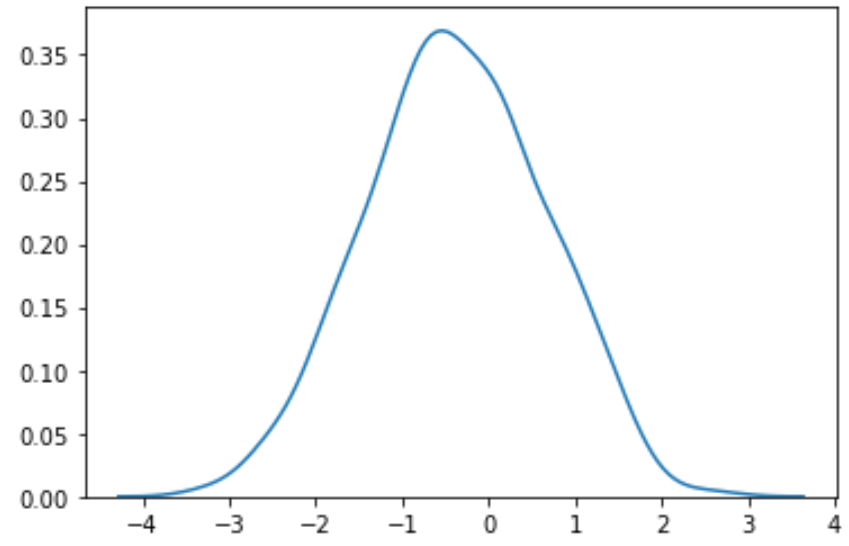
我们可以看到转换后的数据遵循更加正态的分布。

我们还可以找到用于执行 Box-Cox 变换的精确 lambda 值：

 #display optimal lambda value
print (best_lambda)

0.2420131978174143

发现最佳 lambda 约为0.242 。

因此，每个数据值都使用以下等式进行转换：

新 = (旧^0.242 – 1) / 0.242

我们可以通过查看原始数据与转换后数据的值来确认这一点：

 #view first five values of original dataset
data[0:5]

array([0.79587451, 1.25593076, 0.92322315, 0.78720115, 0.55104849])

#view first five values of transformed dataset
transformed_data[0:5]

array([-0.22212062, 0.23427768, -0.07911706, -0.23247555, -0.55495228])

原始数据集中的第一个值是0.79587 。因此，我们应用以下公式来转换该值：

新 = (.79587 ^0.242 – 1) / 0.242 = -0.222

我们可以确认转换后的数据集中的第一个值确实是-0.222 。

其他资源

如何在 Python 中创建和解释 QQ 图
如何在 Python 中执行 Shapiro-Wilk 正态性检验