箱须图

本文解释什么是箱线图，也称为箱线图（或箱线图）。您将了解如何制作这些类型的统计图，以及盒须图及其解释的解决练习。

什么是盒须图？

箱线图也称为箱线图或箱线图，是使用四分位数直观地表示一组统计数据的图形。

箱须图的主要特点是它可以让您快速可视化一系列数据的分散情况，因为它指示数据的四分位数、中位数、极值和异常值。

因此，这种类型的图表由一个矩形框和几条线（或须线）组成，从中出现以下值：

• 框的边界表示第一和第三四分位数（Q ₁和 Q ₃ ）。框内的垂直线是中位数（相当于第二个四分位数_Q2 ）。
• 晶须（或臂）的极限是极值，即数据系列的最小值和最大值。
• 须线之外的点是异常值，或者换句话说，数据可能测量不正确，因此不应在统计研究中考虑。

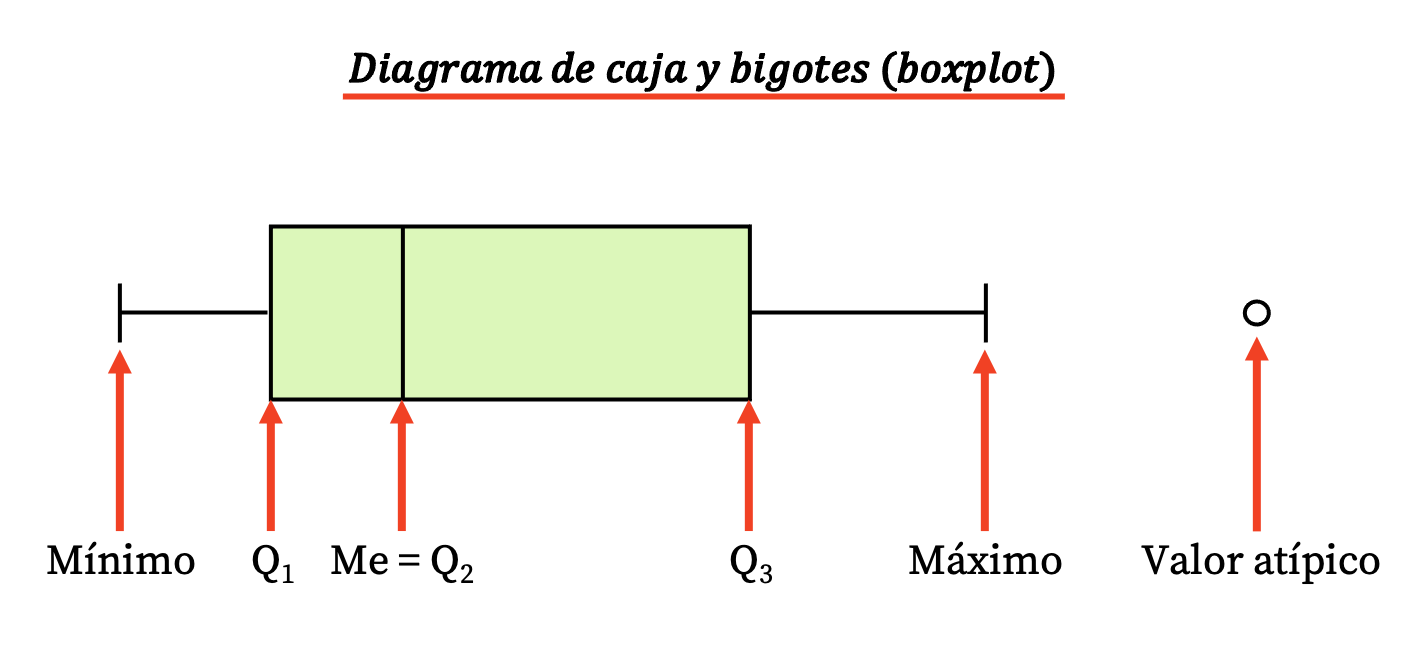
请注意，第三个四分位数和第一个四分位数之间的差异是四分位距（或四分位距），这是统计离散度的另一种度量。

箱线图和须线图对于比较数值变量非常有用。但是，它不适合表示分类变量。

如何创建箱须图

要从数据系列创建箱须图（或箱线图），必须执行以下步骤：

1. 整理统计数据示例。
2. 计算四分位数（Q ₁ 、Q ₂和 Q ₃ ）并将它们表示为图中的方框。第一个和第三个四分位数对应于框的限制，为了表示中位数（第二个四分位数），您必须在其值所在的框内画一条线。
3. 计算四分位数间距，等于第三个四分位数减去第一个四分位数。



4. 计算允许值LI和LS，其公式为：





5. 识别样本异常值，即小于 LI 或大于 LS 的值。用点表示晶须范围之外的这些值。
6. 识别并表示极值，即 LI 和 LS 形成的区间中的最小值和最大值。这些值代表图中两条胡须的末端。

箱须图示例

考虑到箱须图（或箱线图）的定义和理论，您将在下面找到一个具体示例，以更好地理解该概念并了解如何执行此类统计图。

• 绘制以下统计数据集的箱线图。

在本例中，数据已按从小到大的顺序排列，因此无需进行任何更改。否则，我们应该先对样本数据进行排序。

其次，我们提取样本的四分位数：

一旦我们计算了三个四分位数，我们就可以通过减去四分位数 3 减去四分位数 1 来找到四分位数间距：

我们现在计算 LI 和 LS 限值，这些值是数据被视为非典型的值。为此，您必须使用以下公式：

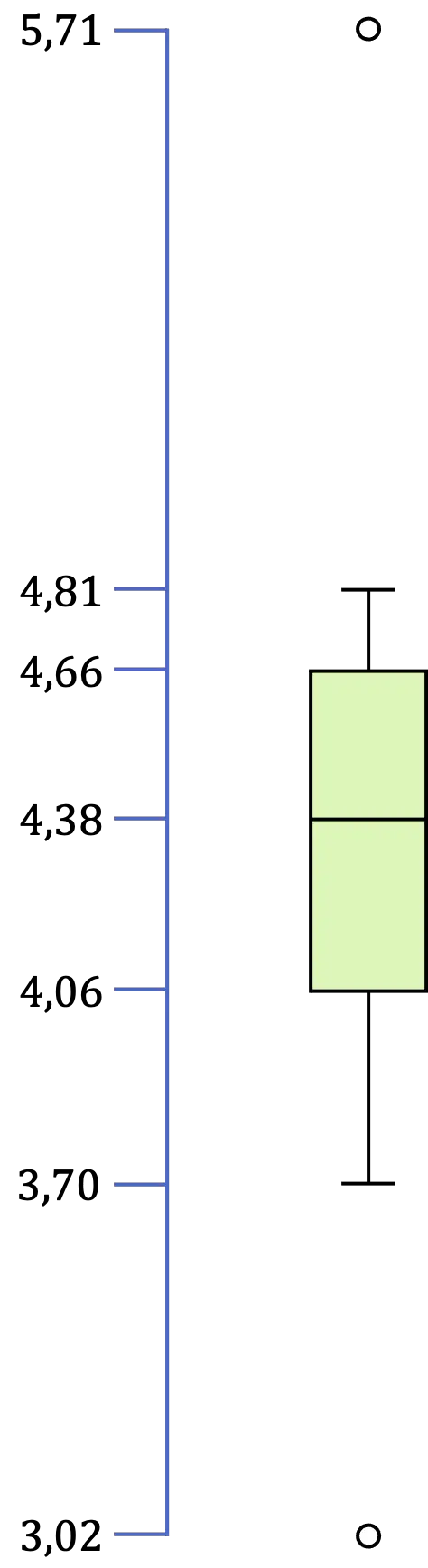
因此，在这种情况下，我们有两个异常值，因为 3.02 小于 3.16，而 5.71 大于 5.56。

最后，仍然需要确定极值，即区间 [LI,LS] 中所有数据的最小值和最大值。因此，在我们的示例中，最小值为 3.70，最大值为 4.81。

因此，一旦我们确定了盒子和胡须图的所有值，剩下的就是进行图形表示：

箱须图的用途是什么？

最后，让我们看看它的用途以及如何解释箱须图（或箱线图）。

显然，箱线图对于快速了解数据系列的四分位数、四分位距、中位数、极值和异常值非常有用，因为所有这些统计度量都可以通过简单的查看来识别。

此外，箱须图用于分析统计样本的对称性，因为它直观地表示了整个数据集。如果中位数不在框的中心，则表示样本不对称。

同样，箱线图在股票市场中广泛用于表示股票价格在一段时间内的变化，因为它们可以让人们看到短时间内的最大值、最小值和中间值。时间，从而做出更快的决策。