累积相对频率

本文解释了统计学中的累积相对频率。因此，您将找到累积相对频率的定义、如何获得累积相对频率以及逐步解决的两个练习。

什么是累积相对频率？

在统计学中，累积相对频率是相对频率的累积和。即一个值的累积相对频率等于该值的相对频率加上所有小于它的值的相对频率。

累积相对频率的符号是H _i 。然而，在统计中，对于此类频率的符号尚未达成完全共识，这就是为什么您还可能会发现它使用其他符号来表示。

显然，要理解累积相对频率的含义，首先必须明确相对频率的概念，这就是为什么我建议您在继续解释之前访问以下链接：

如何计算累积相对频率

要计算累积相对频率，必须遵循以下步骤：

1. 使用统计样本中的所有不同值构建频率表。
2. 计算每个值的绝对频率。
3. 根据绝对频率，确定每个值的相对频率。
4. 找到每个值的累积相对频率，该频率是通过将该值本身的相对频率加上所有较小值的相对频率相加来计算的。

请记住，如果要计算累积相对频率百分比，即以百分比表示的累积相对频率，只需按照相同的步骤将结果乘以 100 即可。

累积相对频率的示例

为了让您了解如何计算累积相对频率，下面显示了逐步解决的两个示例。在第一个示例中，我们找到离散变量的累积相对频率，在第二个示例中，我们找到连续变量的累积相对频率，因为过程略有不同。

示例1：离散变量

• 班级 30 名学生的统计科目成绩如下。每个音符的累积相对频率是多少？

在这种情况下，变量是离散的，因为它不能采用十进制值。因此不需要按区间对数据进行分组，而是可以直接进行计算。

因此，我们绘制一个频率表并确定每个不同值的绝对频率：

接下来，我们计算每个值的相对频率（您可以在文章开头的链接中看到这是如何完成的）。

一旦我们计算了数据集的绝对频率和相对频率，我们就可以得到累积相对频率。为此，我们必须将相关值的相对频率加上所有先前的相对频率，或者换句话说，先前累积的相对频率：

简而言之，有绝对频率、相对频率和累积相对频率的频率表如下：

请记住，累积相对频率的最后一个值应始终为 1。如果您得到另一个数字，则意味着您在计算中犯了错误。

示例 2：连续变量

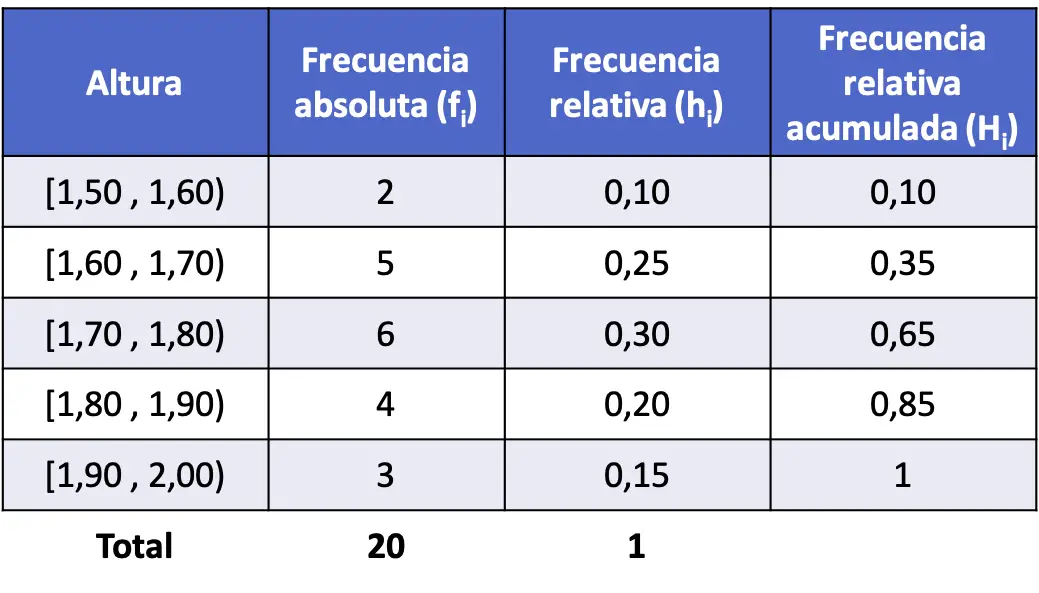
• 测量了 20 个人的身高，得到如下结果。将数据分成多个区间，并找出每个区间的累积相对频率。

这种情况与上一个问题不同，因为数字是十进制的，这意味着变量可以取任何值，因此是连续的。因此，我们将通过将数据分组为间隔来创建频率表。

因此，我们构建表格并获得每个区间的绝对频率：

现在，我们通过将每个间隔的绝对频率除以数据点总数来计算相对频率：

最后，我们找到所有间隔的累积相对频率。与之前一样，要确定某个区间的累积相对频率，需要将所述区间的相对频率加上之前的相对频率相加：

累积相对频率和累积绝对频率

我们刚刚看到了如何从相对频率导出累积相对频率。然而，这种类型的频率也可以使用累积绝对频率来找到。

累积相对频率可以通过将累积绝对频率除以样本中的数据总数来计算。

因此，累积相对频率的公式为：

金子：

• 

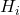
  是累积相对频率。

• 

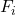
  是累积的绝对频率。

• 

  是数据总数。

按照上面开发的第一个示例，以下是如何从累积绝对频率找到累积相对频率：

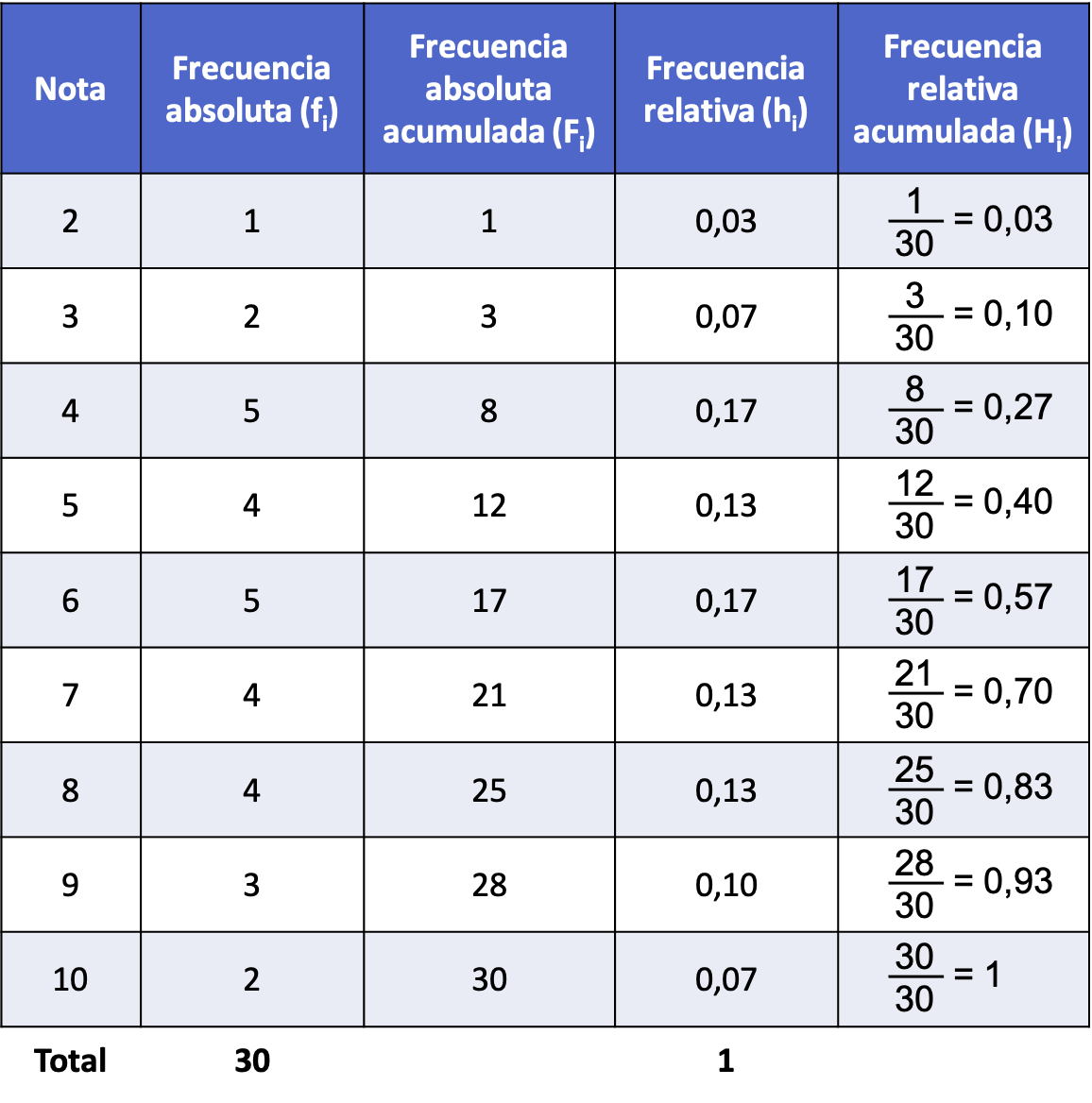
上表由于包含了所有类型的统计频率，因此称为频率表。请点击这里了解更多：