线性回归的四个假设

线性回归是一种有用的统计方法，我们可以用它来理解两个变量 x 和 y 之间的关系。然而，在进行线性回归之前，我们必须首先确保满足四个假设：

1.线性关系：自变量x和因变量y之间存在线性关系。

2. 独立性：残差是独立的。特别是，时间序列数据中的连续残差之间不存在相关性。

3.同方差性：残差在x的每个水平上具有恒定的方差。

4. 正态性：模型残差呈正态分布。

如果这些假设中的一个或多个不满足，那么我们的线性回归的结果可能不可靠，甚至具有误导性。

在本文中，我们对每个假设进行了解释，如何确定假设是否满足，以及如果不满足假设该怎么办。

假设1：线性关系

解释

线性回归的第一个假设是自变量x和自变量y之间存在线性关系。

如何确定这个假设是否满足

检测是否满足此假设的最简单方法是创建 x 与 y 的散点图。这使您可以直观地看到两个变量之间是否存在线性关系。如果图上的点看起来可能沿着一条直线，则两个变量之间存在某种类型的线性关系，并且满足此假设。

例如，下图中的点看起来落在一条直线上，表明 x 和 y 之间存在线性关系：

然而，下图中 x 和 y 之间似乎不存在线性关系：

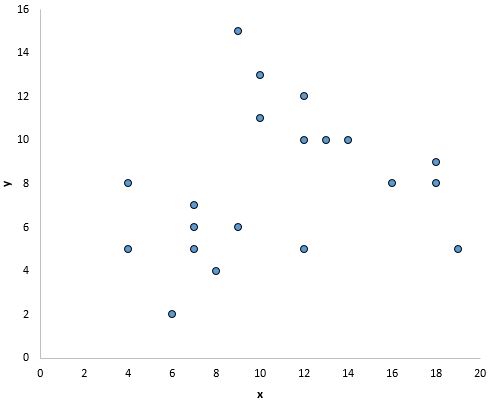
在这张图中，x 和 y 之间似乎存在明显的关系，但不是线性关系：

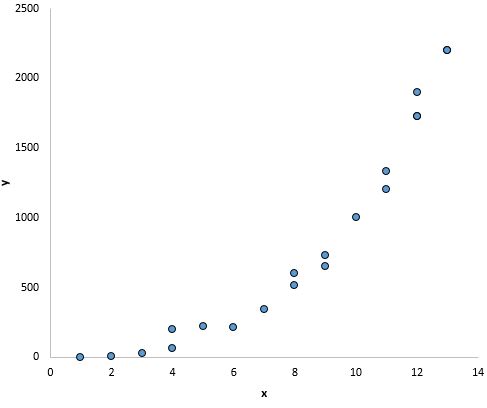
如果不遵守此假设该怎么办

如果您创建 x 和 y 值的散点图并发现两个变量之间不存在线性关系，您有多种选择：

1.对自变量和/或因变量应用非线性变换。常见的示例包括取自变量和/或因变量的对数、平方根或倒数。

2.将另一个自变量添加到模型中。例如，如果 x 与 y 的图具有抛物线形状，则在模型中添加 X ²作为附加自变量可能是有意义的。

假设2：独立性

解释

线性回归的下一个假设是残差是独立的。这在处理时间序列数据时尤其重要。理想情况下，我们不希望连续残差之间存在趋势。例如，残留物不应随时间持续增加。

如何确定这个假设是否满足

测试此假设是否成立的最简单方法是查看残差时间序列图，该图是残差与时间的关系图。理想情况下，大多数残差自相关应落在零附近的 95% 置信带内，这些置信带大约位于n的平方根上的 +/- 2 处，其中n是样本大小。您还可以使用Durbin-Watson 检验正式测试是否满足此假设。

如果不遵守此假设该怎么办

根据违反此假设的方式，您有多种选择：

• 对于正序列相关，请考虑向模型添加因变量和/或自变量的滞后。
• 对于负序列相关，请确保没有任何变量过度延迟。
• 对于季节性相关性，请考虑向模型添加季节性虚拟变量。

假设3：同方差

解释

线性回归的下一个假设是残差在 x 的每个水平上具有恒定方差。这称为同方差性。如果情况并非如此，残差就会出现异方差。

当回归分析中存在异方差时，分析结果变得难以相信。具体来说，异方差增加了回归系数估计值的方差，但回归模型并未考虑到这一点。这使得回归模型更有可能声称模型中的某个项具有统计显着性，而实际上并非如此。

如何确定这个假设是否满足

检测异方差的最简单方法是创建拟合值/残差图。

将回归线拟合到数据集后，您可以创建一个散点图，显示模型的拟合值与这些拟合值的残差。下面的散点图显示了拟合值与残差的典型图，其中存在异方差。

请注意，随着拟合值的增加，残差如何越来越分散。这种“圆锥”形状是异方差的典型标志：

如果不遵守此假设该怎么办

校正异方差的常用方法有以下三种：

1. 变换因变量。常见的转换是简单地取因变量的对数。例如，如果我们使用人口规模（自变量）来预测城市中花店的数量（因变量），我们可以尝试使用人口规模来预测城镇中花店数量的对数。使用因变量的对数而不是原始因变量通常会导致异方差消失。

2. 重新定义因变量。重新定义因变量的常见方法是使用比率而不是原始值。例如，我们可以使用人口规模来预测人均花店数量，而不是使用人口规模来预测一个城市的花店数量。在大多数情况下，这减少了较大人群中自然发生的变异性，因为我们测量的是每人的花店数量，而不是花店本身的数量。

3. 使用加权回归。校正异方差的另一种方法是使用加权回归。这种类型的回归根据拟合值的方差为每个数据点分配权重。本质上，这为具有较高方差的数据点赋予了较低的权重，从而减少了它们的残差平方。当使用适当的权重时，可以消除异方差问题。

假设4：正态性

解释

线性回归的下一个假设是残差呈正态分布。

如何确定这个假设是否满足

有两种常见的方法来检查这个假设是否满足：

1. 使用QQ 图直观地验证假设。

QQ 图是分位数-分位数图的缩写，是一种图，我们可以用它来确定模型的残差是否服从正态分布。如果图上的点大致形成一条直线对角线，则满足正态性假设。

下面的 QQ 图显示了一个大致服从正态分布的残差示例：

然而，下面的 QQ 图显示了残差明显偏离直线对角线的情况示例，表明它们不服从正态分布：

2.您还可以使用正式的统计检验（例如 Shapiro-Wilk、Kolmogorov-Smironov、Jarque-Barre 或 D’Agostino-Pearson）来检查正态性假设。但是，请记住，这些检验对大样本量很敏感 – 也就是说，当样本量很大时，它们通常会得出残差不正常的结论。这就是为什么简单地使用 QQ 图等图形方法来验证这一假设通常更容易。

如果不遵守此假设该怎么办

如果不满足正态性假设，您有多种选择：

• 首先，检查异常值是否对分布产生巨大影响。如果存在任何异常值，请确保它们是真实值而不是数据输入错误。
• 然后，您可以对自变量和/或因变量应用非线性变换。常见的示例包括取自变量和/或因变量的对数、平方根或倒数。

进一步阅读：

简单线性回归简介
了解回归分析中的异方差性
如何在 R 中创建和解释 QQ 图