如何在 ti-84 计算器上执行线性回归

线性回归是一种我们可以用来理解解释变量 x 和响应变量 y 之间关系的方法。

本教程介绍如何在 TI-84 计算器上执行线性回归。

示例：TI-84 计算器上的线性回归

假设我们想要了解学生为考试学习的小时数与考试成绩之间的关系。

为了探索这种关系，我们可以在 TI-84 计算器上执行以下步骤，使用学习时间作为解释变量，考试成绩作为响应变量来执行简单的线性回归。

第 1 步：输入数据。

首先，我们将输入解释变量和响应变量的数据值。按统计，然后按编辑。在 L1 列中输入解释变量（学习时数）的以下值，并在 L2 列中输入响应变量（考试分数）的值：

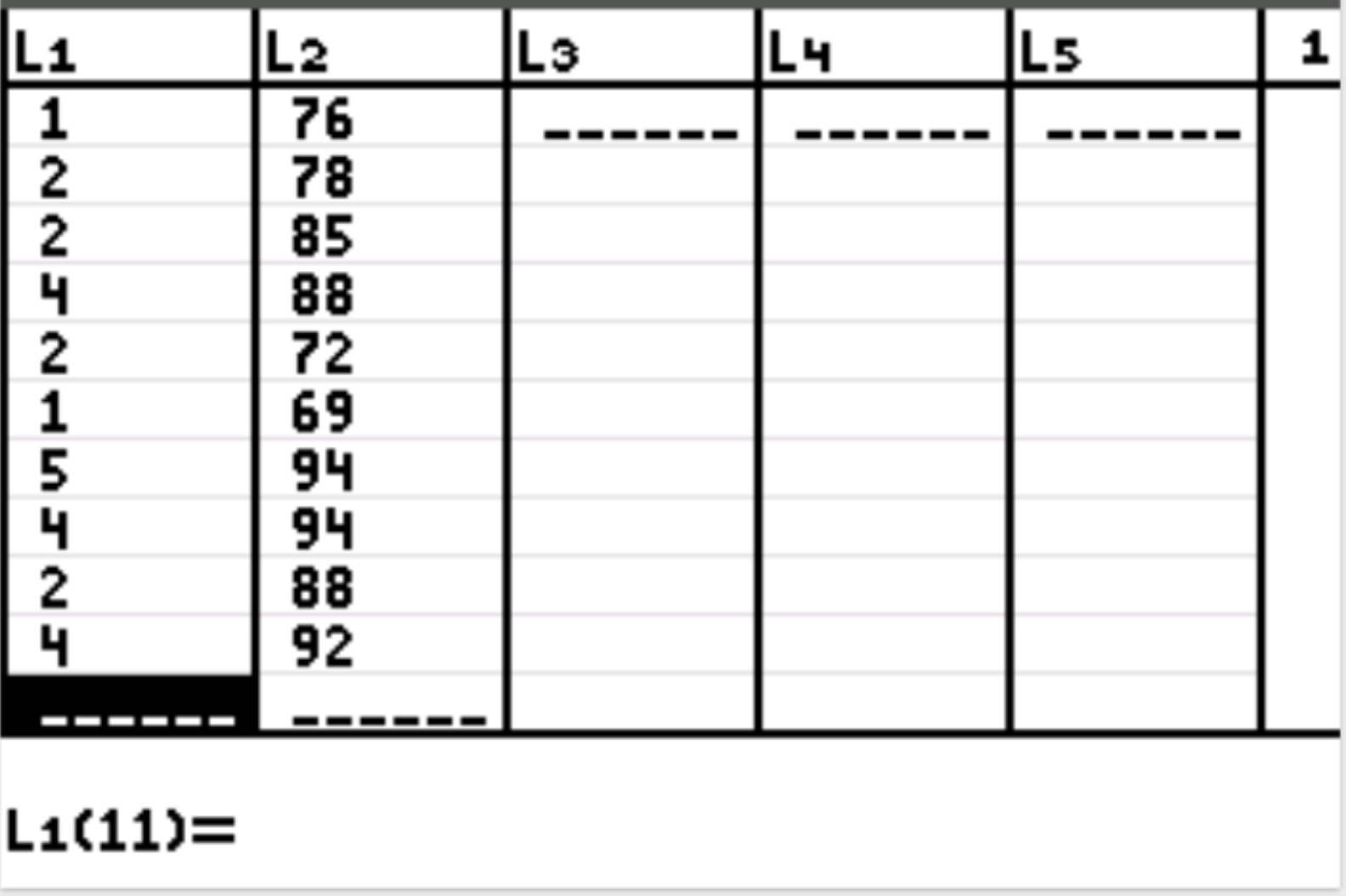
步骤 2：执行线性回归。

接下来，我们将执行线性回归。按Stat ，然后滚动至CALC 。然后滚动到8: Linreg(a+bx)并按Enter 。

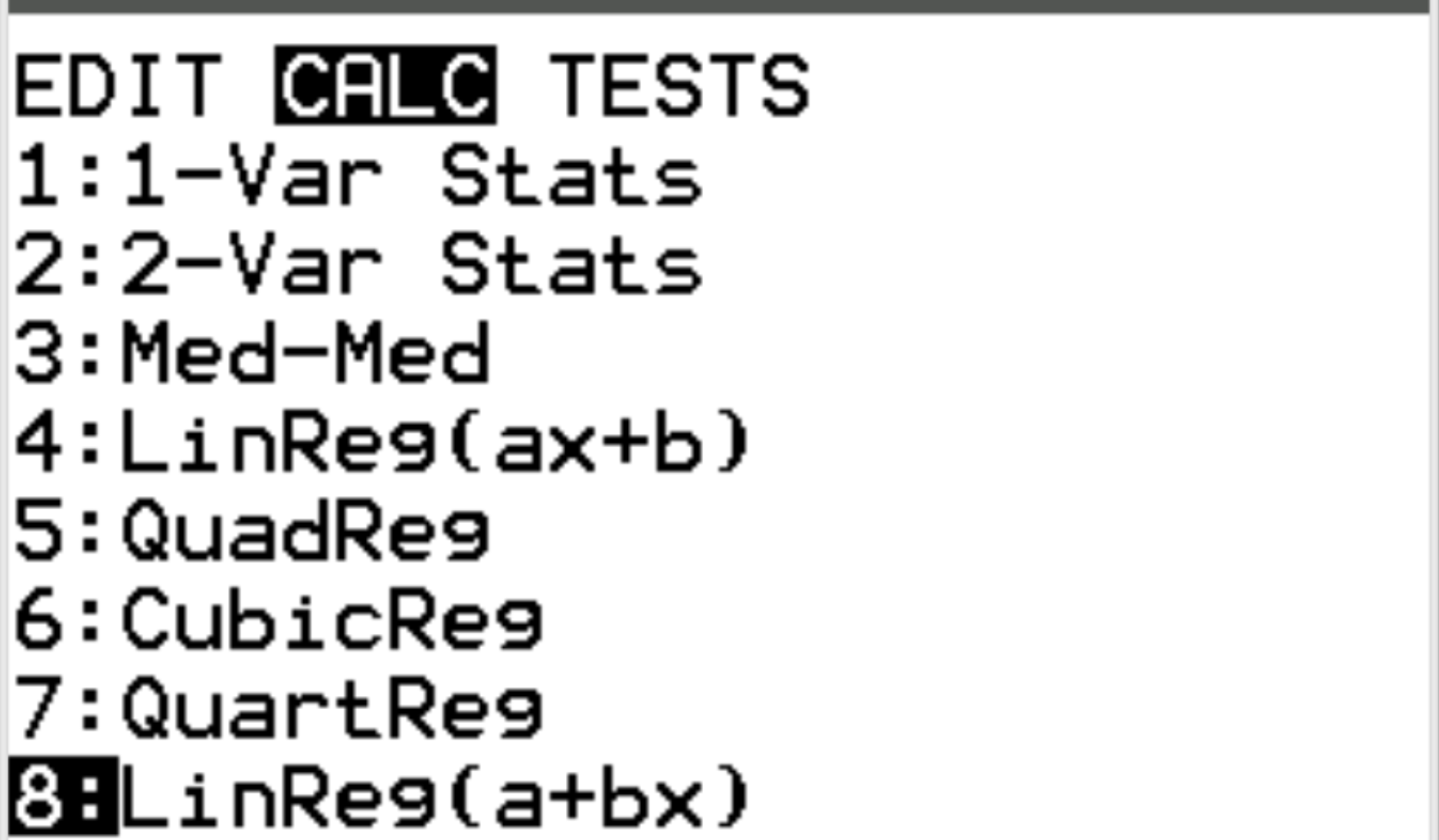
对于 Xlist 和 Ylist，请确保选择 L1 和 L2，因为这些是我们用来输入数据的列。将FreqList留空。向下滚动到计算并按Enter 。将自动出现以下输出：

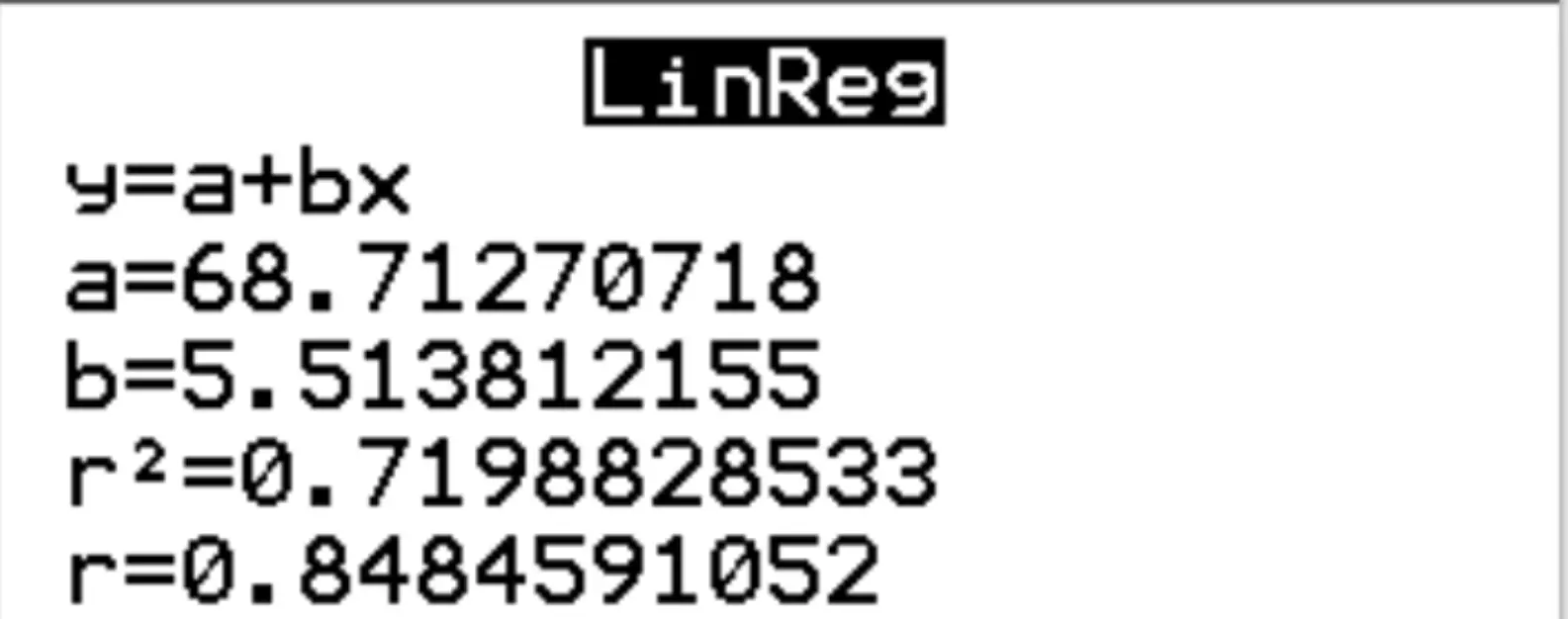
第 3 步：解释结果。

从结果中我们可以看出，估计的回归方程为：

考试成绩 = 68.7127 + 5.5138*（小时）

我们将学时系数解释为每多学习一小时，考试成绩平均应增加5.5138 。我们将截距系数解释为学习零小时的学生的预期考试成绩为68.7127 。

我们可以使用这个估计的回归方程根据学习小时数计算学生的预期考试成绩。

例如，学习三个小时的学生应获得85.25的考试成绩：

考试成绩 = 68.7127 + 5.5138*(3) = 85.25

我们还可以看到回归模型的 r 平方为 r ² = 0.7199 。

该值称为决定系数。它是响应变量中可以由解释变量解释的方差的比例。在此示例中，71.99% 的考试成绩差异可以通过学习时数来解释。

其他资源

如何在 TI-84 计算器上创建残差图
如何在 TI-84 计算器上执行二次回归
如何在 TI-84 计算器上执行指数回归
如何在 TI-84 计算器上执行对数回归