类内相关系数：定义+示例

组内相关系数(ICC) 用于衡量有两个或更多评估者的研究中分数的可靠性。

ICC 的值范围为 0 到 1，其中 0 表示评估者之间没有可靠性，1 表示评估者之间完全可靠。

简单地说，ICC 用于确定不同评分者是否可以对项目（或主题）进行可靠评分。

可以计算多种不同版本的 ICC，具体取决于以下三个因素：

• 模型：单向随机效应、双向随机效应或双向混合效应
• 关系类型：一致性或绝对一致
• 单位：单个评估者或评估者的平均值

以下是三种不同模型的简要说明：

1. 单向随机效应模型：该模型假设每个受试者都由不同组的随机选择的评估者进行评估。在这个模型中，评估者被认为是随机效应的来源。这种模式在实践中很少使用，因为通常使用同一组评估员来评估每个科目。

2.双向随机效应模型：该模型假设从总体中随机选择一组评分者k ，然后用于对受试者进行评分。使用此模型，评估者和受试者被视为随机效应的来源。当我们想要将我们的结果推广给与研究中使用的类似的评估者时，通常会使用此模型。

3.双向混合效应模型：该模型还假设从总体中随机选择一组评分者k ，然后用于对受试者进行评分。然而，该模型假设我们选择的评估者群体是唯一感兴趣的评估者，这意味着我们不希望将我们的结果推广到可能也与研究中使用的评估者具有相似特征的其他评估者。

以下是我们可能想要衡量的两种不同类型关系的简要描述：

1. 一致性：我们对评委评分之间的系统性差异感兴趣（例如，评委对相似主题的评分是否为低和高？）

2. 绝对一致：我们感兴趣的是评委分数之间的绝对差异（例如，评委A和评委B的分数之间的绝对差异是多少？）

以下是我们可能感兴趣的两个不同单位的简要描述：

1. 单一审稿人：我们只想使用单一审稿人的评分作为衡量的基础。

2、评分者平均分：我们想用所有评委评分的平均值作为衡量的基础。

注意：如果您想衡量两个在二分结果中漏掉每个项目的评估者之间的一致性程度，您应该使用Cohen 的 Kappa 。

如何解释组内相关系数

根据Koo & Li 的说法，以下是如何解释类内相关系数的值：

• 小于0.50：可靠性差
• 0.5 到 0.75 之间：中等可靠性
• 0.75至0.9之间：可靠性良好
• 大于0.9：可靠性极佳

下面的例子展示了如何在实践中计算类内相关系数。

示例：组内相关系数的计算

假设请四位不同的评委来评估 10 场不同的高考质量。结果如下所示：

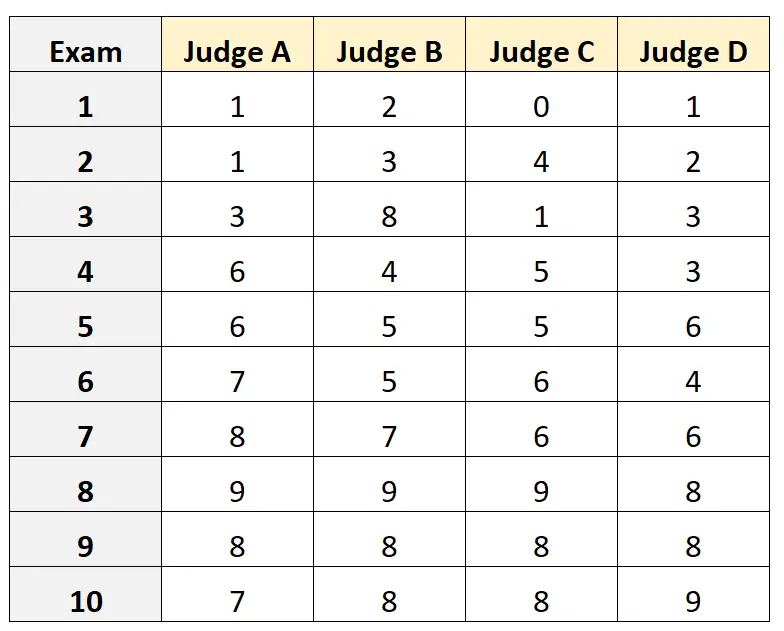
假设四位评委是从一批合格的入学考试评委中随机选出的，我们想要衡量评委之间的绝对一致性，并且我们想使用仅一位评估者角度的分数作为我们衡量的基础。

我们可以在R中使用以下代码来拟合双向随机效应模型，使用绝对一致性作为评分者之间的关系，并使用单个单位作为兴趣单位：

 #load the interrater reliability package
library (irr)

#define data
data <- data. frame (A=c(1, 1, 3, 6, 6, 7, 8, 9, 8, 7),
                   B=c(2, 3, 8, 4, 5, 5, 7, 9, 8, 8),
                   C=c(0, 4, 1, 5, 5, 6, 6, 9, 8, 8),
                   D=c(1, 2, 3, 3, 6, 4, 6, 8, 8, 9))

#calculate ICC
icc(data, model = " twoway ", type = " agreement ", unit = " single ")

   Model: twoway 
   Type: agreement 

   Subjects = 10 
     Failures = 4 
   ICC(A,1) = 0.782

 F-Test, H0: r0 = 0; H1: r0 > 0 
    F(9.30) = 15.3, p = 5.93e-09 

 95%-Confidence Interval for ICC Population Values:
  0.554 < ICC < 0.931

组内相关系数 (ICC) 为0.782 。

根据解释 ICC 的经验法则，我们得出的结论是，ICC 为0.782表明不同评分者可以对考试进行“良好”可靠性评分。

其他资源

以下教程详细讲解了如何在不同的统计软件中计算ICC：

如何在 Excel 中计算类内相关系数
如何在R中计算组内相关系数
如何用Python计算类内相关系数