统计在教育中的重要性（举例）

统计学领域涉及数据的收集、分析、解释和呈现。

在教育领域，统计数据非常重要，原因如下：

原因 1 ：统计允许教育工作者使用描述性统计来了解学生的表现。

原因 2 ：统计数据使教师可以使用数据可视化来发现学生表现的趋势。

原因 3 ：统计数据允许教育工作者使用假设检验来比较不同的教学方法。

在本文的其余部分中，我们将逐一阐述这些原因。

原因 1：使用描述性统计数据了解学生表现

描述性统计用于描述数据。

在教育背景下，教师可以计算班级学生的以下描述性统计数据：

• 给定考试的平均分数。
• 某项考试的分数标准差。
• 给定考试的分数范围。
• 通过某项考试的学生百分比。
• 给定考试成绩的第 90 个百分点。

通过这些测量，老师可以更好地了解班上学生在特定考试中的成绩。

然后，如果通过考试的学生太少，她可以决定是否改变教学方法，或者可能为考试成绩差的学生提供额外的辅导机会等。

注：这些类型的描述性统计用于各级教育。例如，校长可以使用描述性统计来监控整个学校学生的考试成绩。州教育部门还可以使用描述性统计数据来监控整个州学生的考试成绩。

原因 2：使用数据可视化发现趋势

在教育中使用统计数据的另一种常见方法是可视化数据，例如折线图、直方图、箱线图、饼图和其他图表。

这些类型的图表通常用于帮助教育工作者发现课堂表现和学生个人表现的趋势。

例如，假设老师创建以下条形图来可视化全年的平均考试成绩：

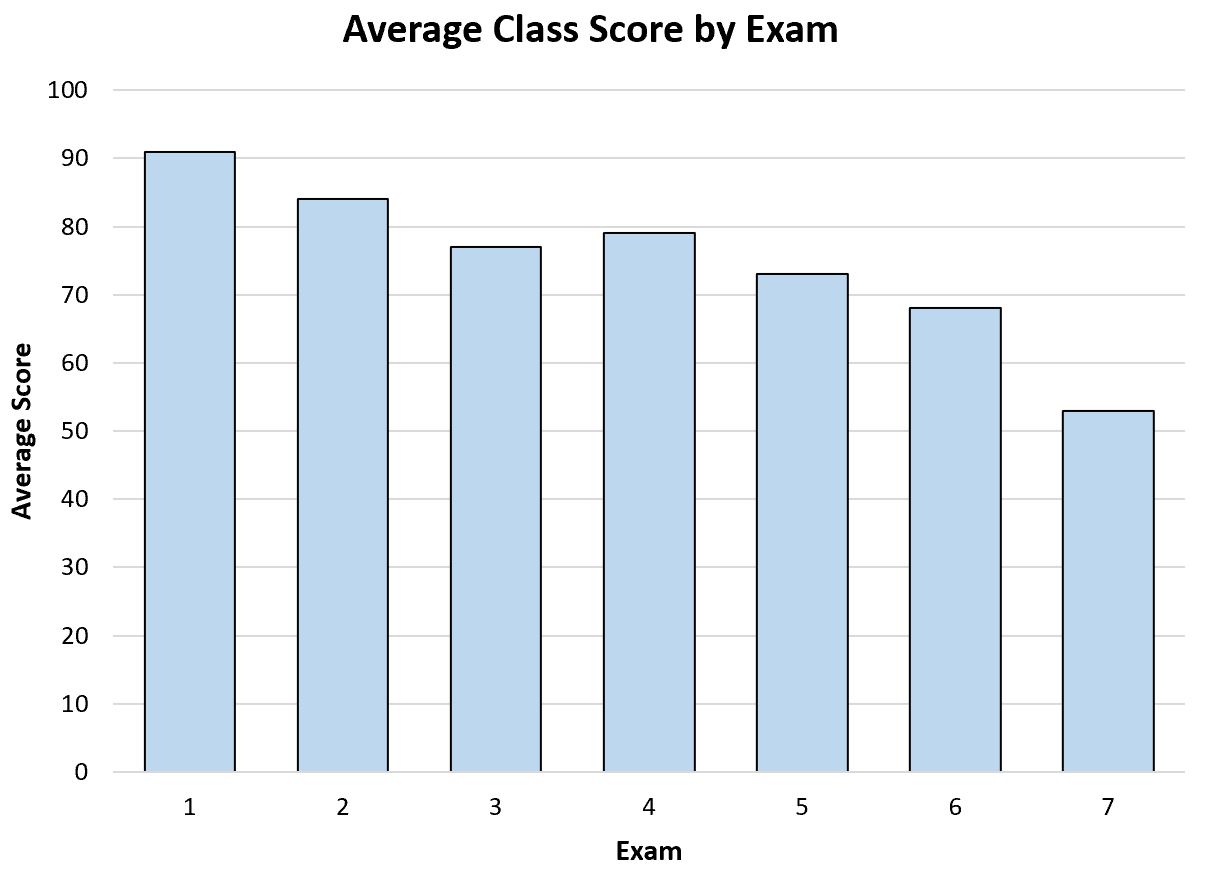
只要看这张条形图，老师就能看到他们班学生的平均考试成绩一年来在慢慢下降。

这可以让老师改进他的教学方法，或者可以给他的学生进行调查，询问他们对他的教学方法的意见等。

原因 3：使用假设检验来比较教学方法

统计学还以假设检验的形式用于教育。

教育工作者可以使用这些测试来确定不同教学方法之间是否存在统计显着性。

例如，假设老师想要确定某个课程是否会影响考试成绩。为了验证这一点，他随机选择了15 名学生进行预测试。然后他让每个学生使用该课程一个月，然后进行类似难度的后测。

15名学生的测试结果如下：

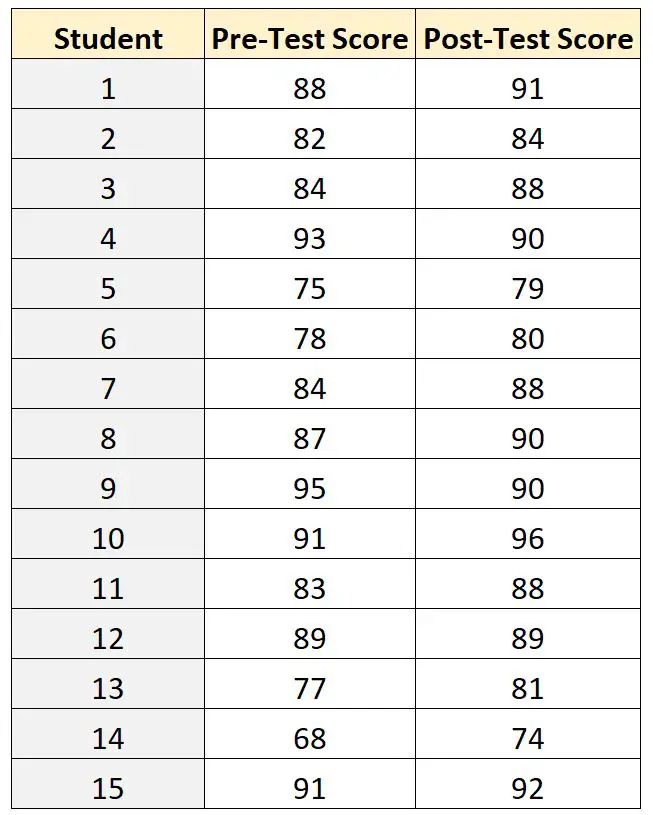
为了比较测试前和测试后平均分数之间的差异，教师可以使用配对 t 测试样本，因为对于每个学生，他们的测试前分数可以与测试后分数相关联。

假设教授使用统计软件执行配对样本 t 检验并收到以下结果：

• t 检验统计量： -2.97
• p 值： 0.0101

在此示例中，配对样本 t 检验使用以下原假设和备择假设：

• H ₀ :测试前和测试后的平均分数相等
• H _A :测试前和测试后的平均分数不相等

由于 p 值 ( 0.0101 ) 小于 0.05，因此我们拒绝原假设。

这意味着我们有足够的证据表明学生在参加学习计划之前和之后的平均考试成绩是不同的。

注意：这只是教育中使用的假设检验的一个例子。其他常见检验包括单样本 t 检验、双样本 t 检验、单向方差分析和双向方差分析。

其他资源

以下文章解释了统计在其他领域的重要性：

统计在企业中的重要性
统计学在经济学中的重要性
统计在医疗保健中的重要性