抽样（统计）

本文解释了什么是统计抽样。此外，您将能够看到如何制作不同类型的样品以及每种样品的示例。

统计学中的抽样是什么？

在统计学中，抽样是选择总体样本的过程。换句话说，抽样是选择一组个体进行统计研究的方法。

例如，一种抽样方法是随机选择个体。因此，如果我们想研究统计总体的规模，我们可以通过简单随机抽样来选择研究样本。

有多种对总体进行抽样的方法，每种方法都有其优点和缺点。下面我们将了解统计抽样的不同类型。

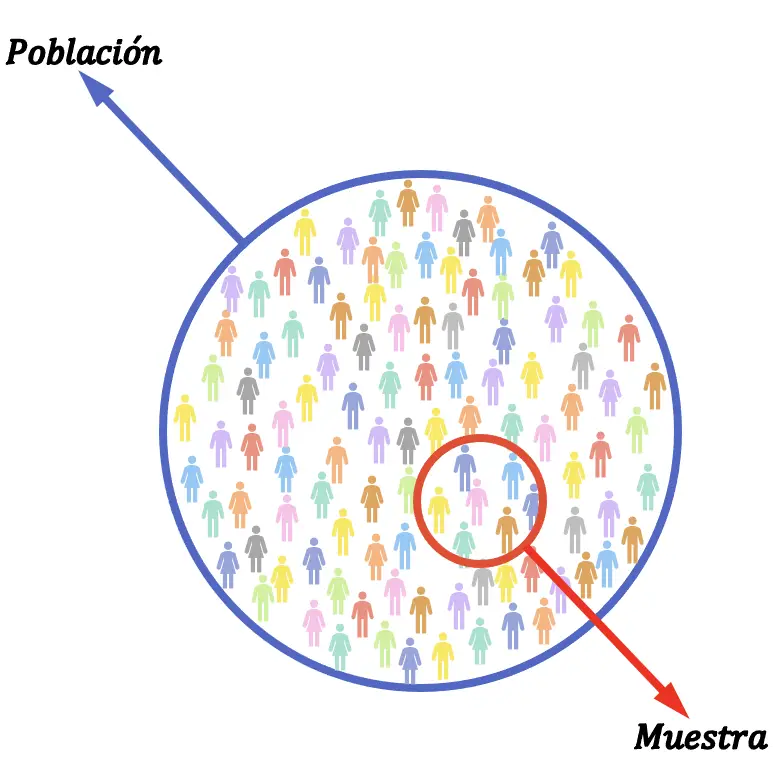
统计学中的抽样非常有用，因为它允许您仅研究目标人群的一部分，然后通过统计推断将分析样本获得的结论推断到整个人群。这是一个很大的优势，因为它减少了搜索时间和成本。

取样架

在统计学中，抽样框（或抽样框）是样本中可以选择的总体中所有元素的列表。换句话说，抽样框是统计研究所针对的宇宙中所有元素的列表。

例如，如果要对某个城市的居民进行统计调查，那么本次研究的抽样框就是该城市的户口簿，因为它是一个包含所有居住在该城市的人口的列表。

因此，抽样框用于获取统计调查的样本。如果抽样框设计得好，抽样进行统计分析就会容易得多。

统计中的抽样类型

在统计中，抽样的类型如下：

• 概率抽样：随机选择样本的抽样。
  • 简单随机抽样：样本是简单随机选择的。
  • 系统抽样：随机选择第一个个体，然后按照固定间隔选择样本的其余元素。
  • 分层抽样：为了构成样本，将目标人群分为不同的层（组），然后从每个层中随机选择个体。
  • 整群抽样：样本由随机选择的簇（自然群体）组成。
• 非概率抽样：研究人员根据其标准选择样本的抽样，过程中不包括机会。
  • 目的抽样：仅根据研究人员的判断从样本中选择个体。
  • 便利抽样：根据访问的难易程度选择样本成员。
  • 连续抽样：选择第一个初始样本并进行研究，然后选择另一个样本。并对不同的样本进行研究，直至得出研究结论。
  • 配额抽样：首先组成小组，然后从每个组中选择一个配额来形成研究样本。
  • 滚雪球抽样：研究人员选择样本中的第一批个体，然后招募其他受试者进行研究。

下面详细解释每种类型的统计抽样。

概率抽样

概率抽样技术包括随机选择样本元素，即它们都具有相同的被选择概率。

这是抽样被认为是概率的必要条件，统计总体的所有元素都必须能够被选择，而且它们必须具有相同的被选择的可能性。

正如我们刚才所看到的，不同类型的概率抽样方法是简单随机抽样、系统抽样、分层抽样和整群抽样。

简单随机抽样

简单随机抽样使统计总体的每个元素都具有相同的概率被纳入研究样本。因此，样本中的个体只是随机选择的，而不使用其他标准。

随机模拟有多种方法，但目前通常使用Excel等计算机程序来完成，因为它们可以节省大量时间。

系统抽样

在系统抽样中，首先随机选择总体中的一个元素，然后使用固定间隔选择样本中的其余元素。

因此，在系统抽样中，一旦我们从样本中随机选择了第一个个体，我们就需要计算所需间隔的数量，以从样本中选择下一个个体。我们依次重复相同的过程，直到样本中的个体数量与我们希望获得的样本量一样多。

分层抽样

在分层抽样技术中，首先将总体分为阶层（群体），然后从每个阶层中随机选择一些个体，形成整个研究样本。因此，样本中每个阶层至少有一名成员。

阶层必须是同质群体，即一个阶层中的个体有自己区别于其他阶层的特征。因此，一个人只能属于一个阶层。

整群抽样

整群抽样和分层抽样可能会混淆，因为它们非常相似，但如果仔细观察，它们是两种不同类型的概率抽样。

整群抽样利用群体中已经存在的自然簇（群体）这一事实，仅研究少数簇而不是群体中的所有个体。

与分层抽样不同，在这种方法中，不需要从集群中选择特定的个体，但一旦选择了要研究的群体，就必须分析其所有成员。

整群抽样又称整群抽样、整群抽样或区域抽样。

非概率抽样

在非概率抽样中，根据研究人员的主观标准选择个体。因此，在非概率抽样中，并非总体中的所有元素都具有相同的被选择作为样本的概率，因为选择不是随机的。此功能将非概率抽样与概率抽样区分开来。

从逻辑上讲，在非概率抽样中，负责进行研究的人非常重要，因为他或她是决定样本中包含谁的人。这就是为什么研究人员必须在研究领域拥有丰富的知识和经验才能获得可靠的结果。

如上所述，不同类型的非概率抽样技术包括目的抽样、便利抽样、连续抽样、配额抽样和滚雪球抽样。

目的性抽样

目的抽样仅依赖于研究者选择研究样本的自由裁量权。

使调查负责人拥有选择样本要素的全部决策权。因此，您是该研究领域的专家非常重要。

目的抽样也称为判断抽样、判断抽样、临界抽样、目的抽样或意见抽样。

简单采样

在便利抽样中，研究人员根据易于接触个体的标准来选择样本对象，过程中不包括机会。

也就是说，在这种从总体中选择个体的非概率抽样中，评估其选择的可用性、接近度或成本等方面。志愿者甚至经常被接受以进一步促进采样。

便利抽样也称为有目的选择抽样或机会抽样。

连续采样

在连续抽样中，首先选择一个初始样本进行研究，在获得初始样本的结果后，再研究另一个样本。并且不断重复这个过程，直到得到整个研究的最终结论。

因此，连续抽样并不关注单个样本，而是研究同一统计总体中的不同样本，并最终根据从所有群体获得的信息得出结论。

配额抽样

在配额抽样中，首先建立具有至少一种特征的个体群体（或阶层），然后从每个群体中选择一个配额，从而形成研究样本。

用于将人群分组的个体特征也是由研究人员决定的，因此，负责进行研究的人对所获得的结果有很大影响。

雪球抽样

在滚雪球抽样中，研究人员选择第一批参与者，然后招募更多个体进行研究。

滚雪球抽样的这一特征会导致样本量不断增加，因为参与者会招募更多的人参与研究（滚雪球效应）。

雪球抽样也称为链式抽样或链式参考抽样。

采样与显示

在统计学中，样本是从总体中选择进行分析的一组个体。也就是说，在整个目标人群中，实际上在进行统计研究时，只分析了一部分人群，称为样本。

因此，抽样和样本之间的区别在于样本是所研究总体的一部分。另一方面，抽样是选择统计研究样本的方法。

因此，抽样在统计学中非常重要，因为它是一种使我们能够从目标群体转向研究样本的技术。

从逻辑上讲，所选样本不能只是任何人，而必须满足某些条件，以便将结论外推到整个人群。例如，为了使样本具有代表性，它必须具有最小大小，这取决于研究的特征。