如何在 stata 中创建相关矩阵

在统计学中，我们经常寻求理解两个变量之间的关系。例如，我们可能想了解学生学习的小时数与考试成绩之间的关系。

量化这种关系的一种方法是使用Pearson 相关系数，它是两个变量之间线性关联的度量。它的值介于 -1 和 1 之间，其中：

• -1 表示两个变量之间完全负线性相关
• 0 表示两个变量之间不存在线性相关
• 1 表示两个变量之间存在完全正线性相关

相关系数离零越远，两个变量之间的相关性越强。

但在某些情况下，我们想要了解多对变量之间的相关性。在这些情况下，我们可以创建一个相关矩阵，它是一个方表，显示变量的多个成对组合之间的相关系数。

在本教程中，我们将解释如何在 Stata 中创建相关矩阵。

如何在 Stata 中创建相关矩阵

corr命令可用于为 Stata 中的特定数据集生成相关矩阵。

为了说明这一点，让我们通过在命令框中键入以下内容将 1980 年人口普查数据加载到 Stata 中：

使用https://www.stata-press.com/data/r13/census13

然后，我们可以通过在命令框中输入以下内容来快速获取数据集的摘要：

总结一下

这会产生下表：

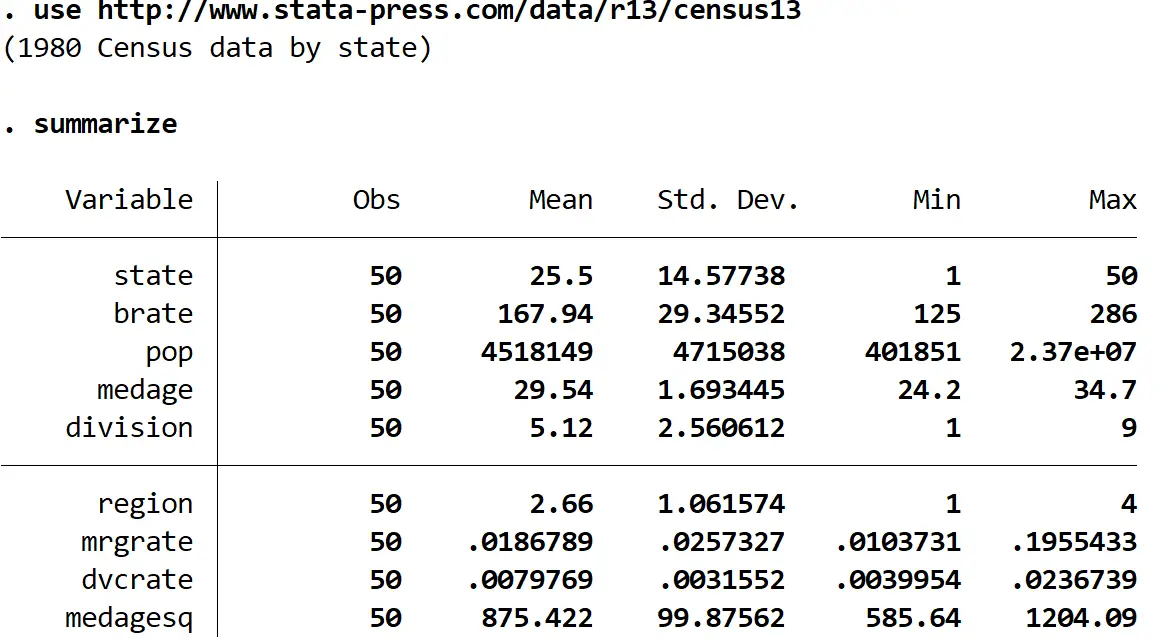
我们看到数据集包含九个不同的变量。要为数据集中变量的每个成对组合创建相关矩阵，我们可以在命令框中输入以下内容：

更正

这会产生以下相关矩阵：

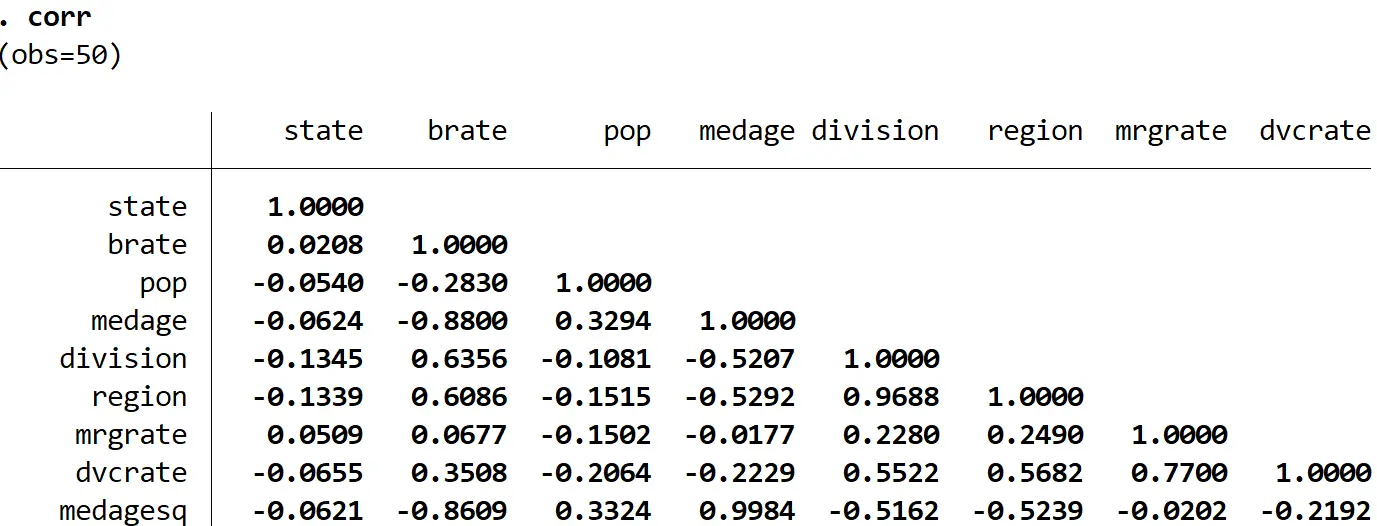
表中显示的数字代表每个变量成对组合的皮尔逊相关系数。例如，人口与州之间的相关性为-0.0540 。这表明这两个变量呈轻微负相关。

请注意，沿表对角线的相关性均为 1.0000，因为每个变量都与其自身完全相关。

您还可以通过在corr命令后指定变量，仅为数据集中的特定变量子集创建相关矩阵。例如，以下是如何仅为pop 、 medage和Region变量创建相关矩阵：

修正流行音乐区域

这仅针对这三个变量生成以下相关矩阵：

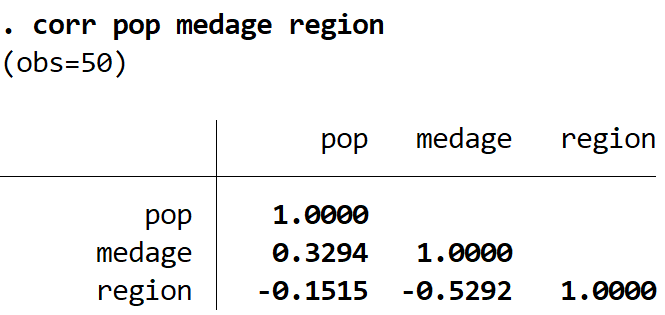
还可以使用pwcorr命令（产生与corr相同的结果）和star()命令，在具有一定显着性水平的统计显着性的相关系数旁边放置一个星号。

例如，以下代码为人口普查数据集中的每个变量生成一个相关矩阵，并在 α = 0.05 处具有统计显着性的相关系数旁边放置一个星号：

pwcorr，星号 (.05)

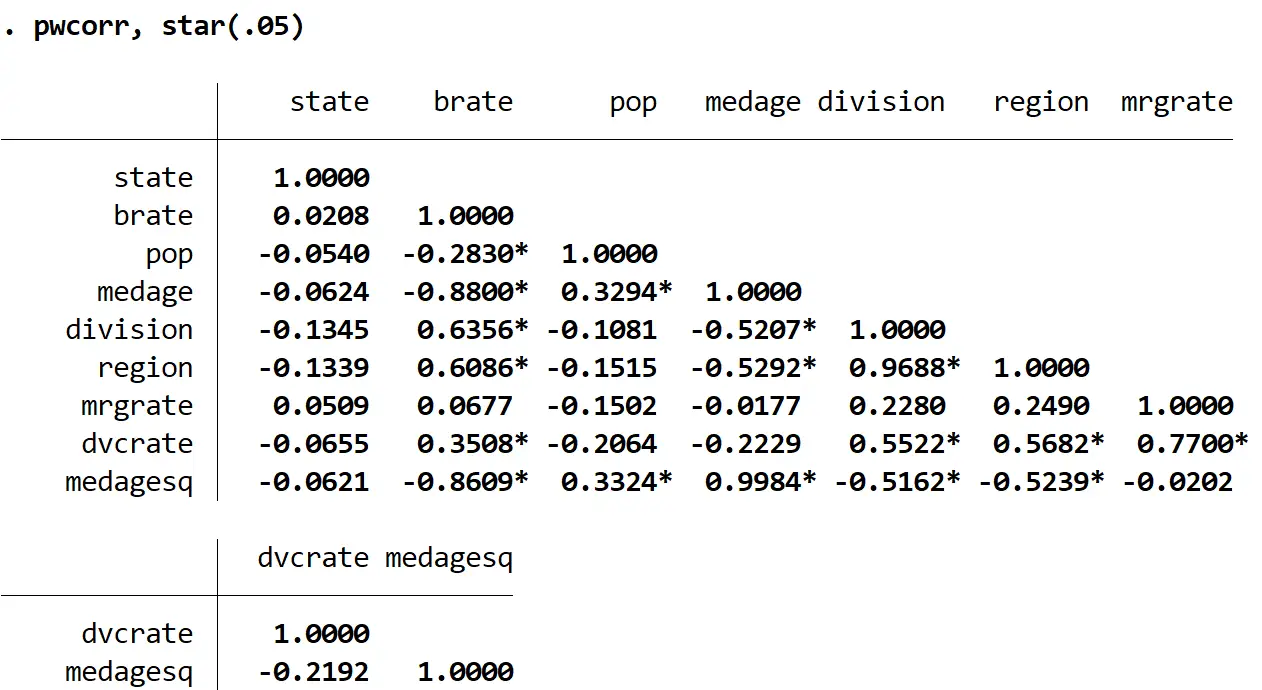
请注意表中的几个相关系数在 α = 0.05 时具有统计显着性。我们可以将 α 设置为我们想要的任何数字，但常见的选择是 0.01、0.05 和 0.10。

一般来说，α 值越低，相关系数的统计显着性越小。例如，假设我们设置 α = 0.01。

pwcorr，星号 (.01)

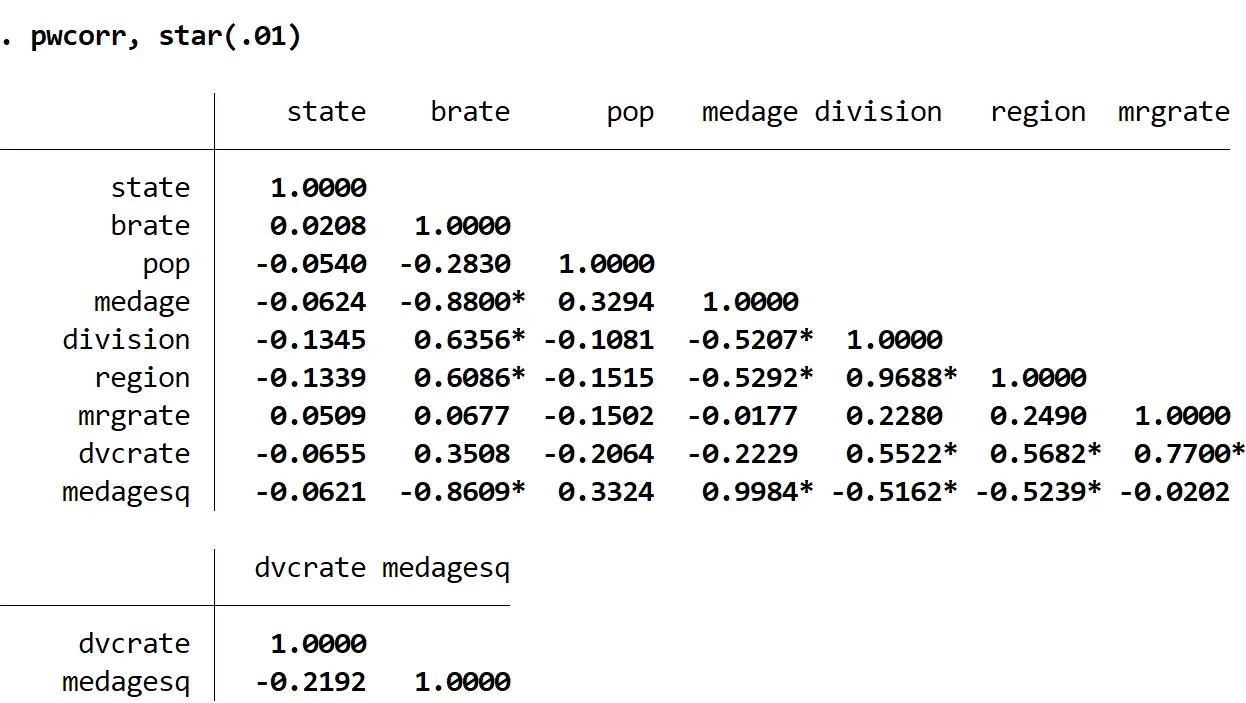
请注意，旁边带有星号的相关系数较少。