如何使用 f 分布创建置信区间

为了确定两个总体的方差是否相等，我们可以计算方差比σ ² ₁ / σ ² ₂ ，其中 σ ² ₁是总体 1 的方差，σ ² ₂是总体 2 的方差。

为了估计真实的总体方差比，我们通常从每个总体中抽取一个简单的随机样本，并计算样本方差比s ₁ ² / s ₂ ² ，其中 s ₁ ²和 s ₂ ²是样本 1 和样本的样本方差。分别为2。

该检验假设 s ₁ ²和 s ₂ ²是根据大小为 n ₁和 n ₂的独立样本计算得出的，这两个样本都来自正态分布总体。

该比率距离 1 越远，群体内差异不平等的证据就越有力。

σ ² ₁ / σ ² ₂的(1-α)100% 置信区间定义为：

(s ₁ ² / s ₂ ² ) * F _{n 1 -1, n 2 -1, α/2} ≤ σ ² ₁ / σ ² ₂ ≤ (s ₁ ² / s ₂ ² ) * F _{n 2 -1, n 1 -1, α/2}

其中 F _{n 2 -1、n 1 -1、α/2}和 F _{n 1 -1、n 2 -1、 α/2}  是所选显着性水平 α 的分布 F 的临界值。

以下示例说明如何使用三种不同的方法创建 σ ² ₁ / σ ² ₂的置信区间：

• 用手
• 使用微软Excel
• R统计软件的使用

对于以下每个示例，我们将使用以下信息：

• α = 0.05
• n ₁ = 16
• _n2 = 11
• s ₁ ² =28.2
• s ₂ ² = 19.3

手动创建置信区间

要手动计算σ ² ₁ / σ ² ₂的置信区间，我们只需将我们拥有的数字代入置信区间公式：

(s ₁ ² / s ₂ ² ) * F _{n1-1, n2-1,α/2} ≤ σ ² ₁ / σ ² ₂ ≤ (s ₁ ² / s ₂ ² ) * F _{n2-1, n1-1, α/2}

我们唯一缺少的数字是临界值。幸运的是，我们可以在分布表 F中找到这些临界值：

F _{n2-1, n1-1, α/2} = F _{10, 15, 0.025} = 3.0602

F _{n1-1, n2-1, α/2} = 1/ F _{15, 10, 0.025} = 1 / 3.5217 = 0.2839

（点击可放大表格）

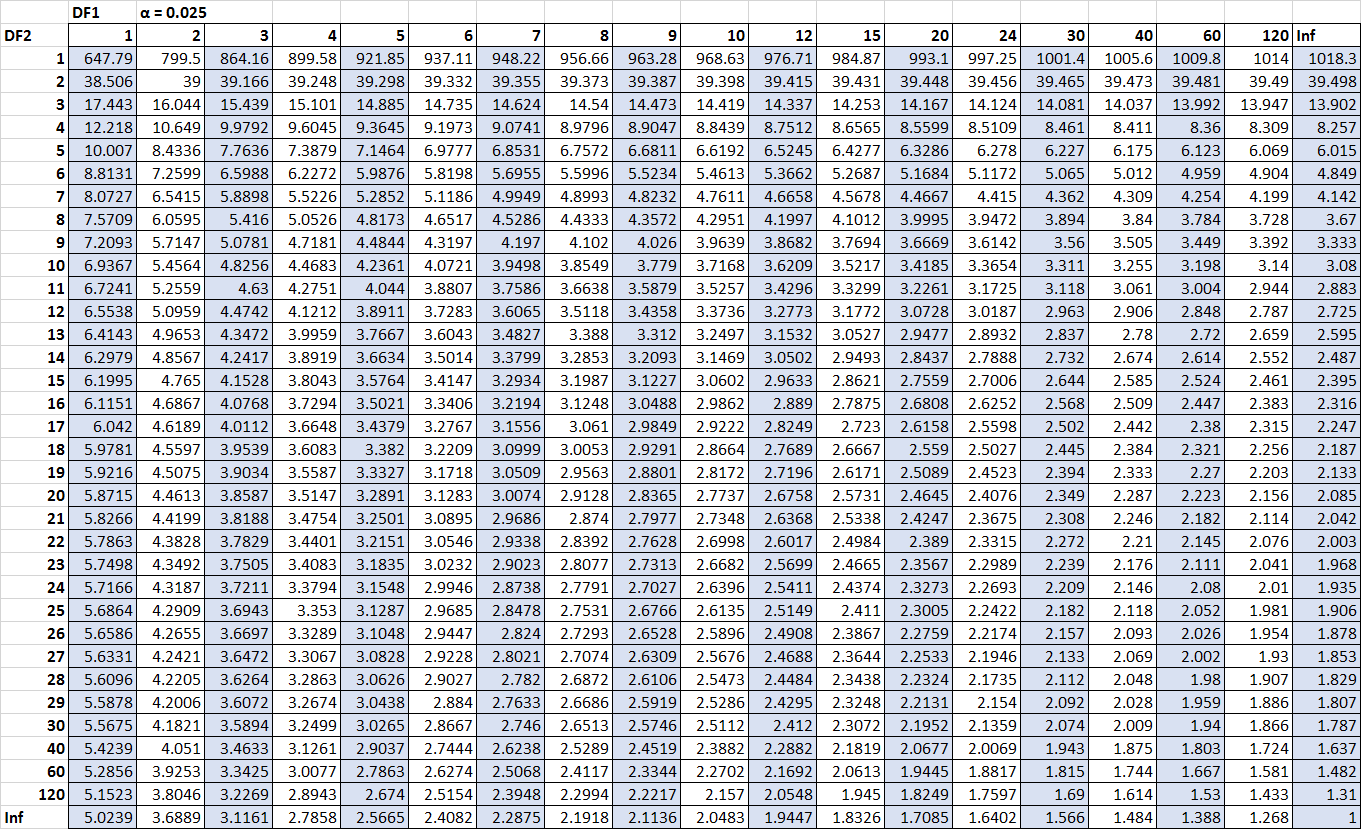
我们现在可以将所有数字代入置信公式区间：

(s ₁ ² / s ₂ ² ) * F _{n1-1, n2-1,α/2} ≤ σ ² ₁ / σ ² ₂ ≤ (s ₁ ² / s ₂ ² ) * F _{n2-1, n1-1, α/2}

(28.2 / 19.3) * (0.2839) ≤ σ ² ₁ / σ ² ₂ ≤ (28.2 / 19.3) * (3.0602)

0.4148 ≤ σ ² ₁ / σ ² ₂ ≤ 4.4714

因此，总体方差比率的 95% 置信区间为(0.4148, 4.4714) 。

使用 Excel 创建置信区间

下图显示了如何在 Excel 中计算总体方差比的 95% 置信区间。置信区间的下限和上限显示在 E 列中，用于查找下限和上限的公式显示在 F 列中：

因此，总体方差比率的 95% 置信区间为(0.4148, 4.4714) 。这与我们手动计算置信区间时得到的结果相符。

使用 R 创建置信区间

以下代码说明了如何计算 R 中总体方差比率的 95% 置信区间：

 #define significance level, sample sizes, and sample variances
alpha <- .05
n1 <- 16
n2 <- 11
var1 <- 28.2
var2 <- 19.3

#define F critical values
upper_crit <- 1/qf(alpha/2, n1-1, n2-1)
lower_crit <- qf(alpha/2, n2-1, n1-1)

#find confidence interval
lower_bound <- (var1/var2) * lower_crit
upper_bound <- (var1/var2) * upper_crit

#output confidence interval
paste0("(", lower_bound, ", ", upper_bound, " )")

#[1] "(0.414899337980266, 4.47137571035219 )"

因此，总体方差比率的 95% 置信区间为(0.4148, 4.4714) 。这与我们手动计算置信区间时得到的结果相符。

其他资源

如何读取F配电盘
Excel中如何求临界值F