什么是聚合偏差？ （解释和示例）

当聚合数据中观察到的趋势被错误地假设也适用于各个数据点时，就会出现聚合偏差。

理解这种偏见的最简单方法是举一个简单的例子。

示例：聚合偏差

假设研究人员想要了解某个州的平均受教育年限与平均家庭收入之间的关系。他们获取了该州 4 个不同城市的汇总数据，并计算了平均教育程度与平均家庭收入之间的相关性。

结果表明，平均受教育年限与平均家庭收入之间的相关性为0.9632 。这是一个非常正的相关系数。

研究人员甚至创建了一个散点图来可视化平均受教育年限与平均家庭收入之间的关系：

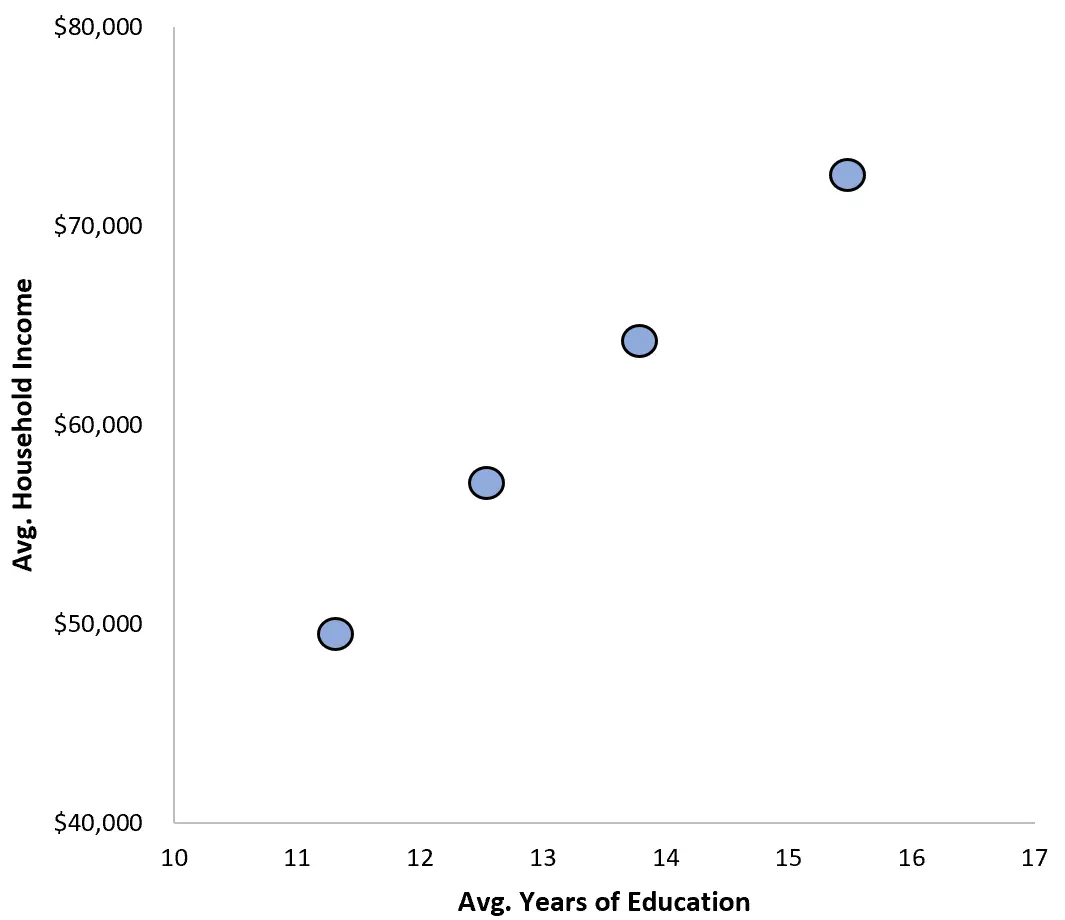
在不实际查看个人数据的情况下，他们可以发布一份报告，声称更长的教育年限与家庭收入呈强烈正相关。

然而，假设一年后一位新研究人员进来并获得了同一组城市中各个家庭的数据。假设她创建了以下数据散点图：

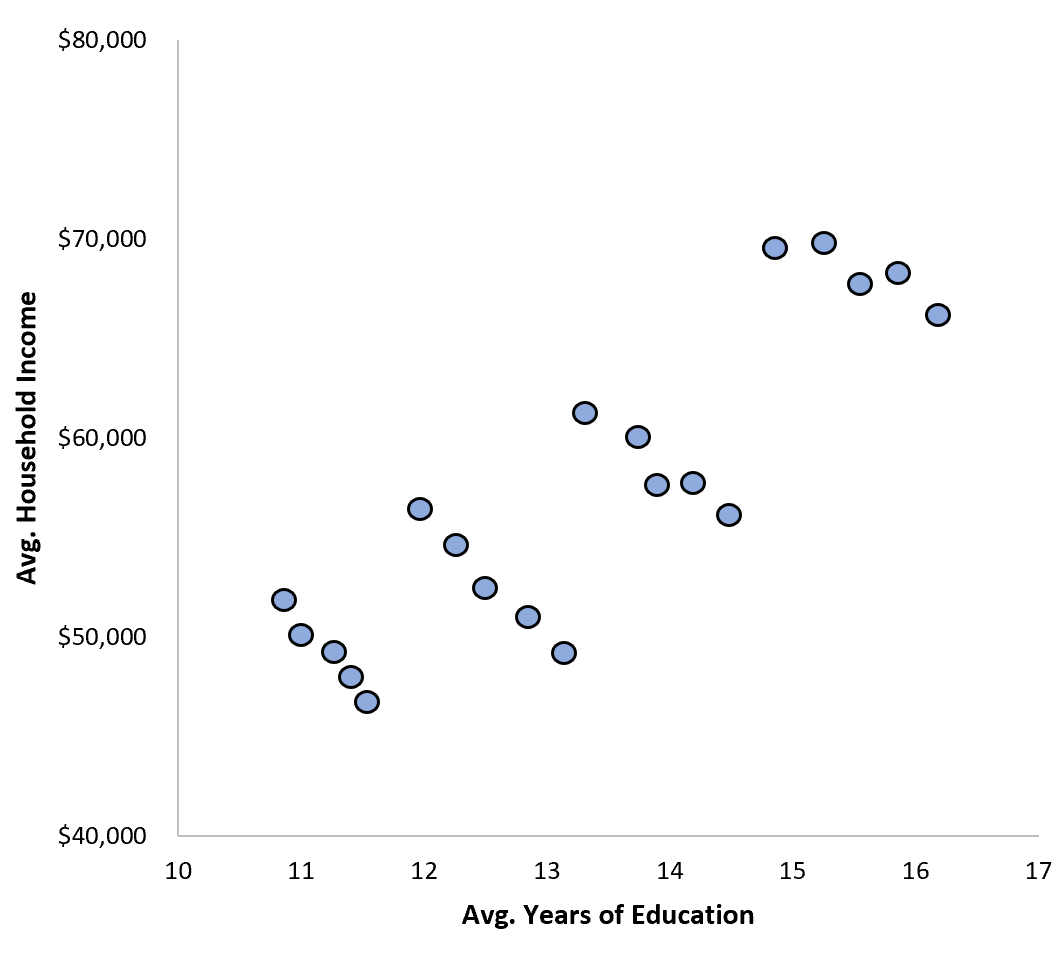
她计算了两个变量之间的相关性，发现实际上只有0.1788——仍然是正相关，但远没有以前研究人员发现的相关性那么强。

事实证明，当数据汇总后，它涵盖了个人层面上教育与收入之间的真实趋势。

事实上，当我们在散点图中逐个城市查看时，教育和收入之间的关系实际上是负的！

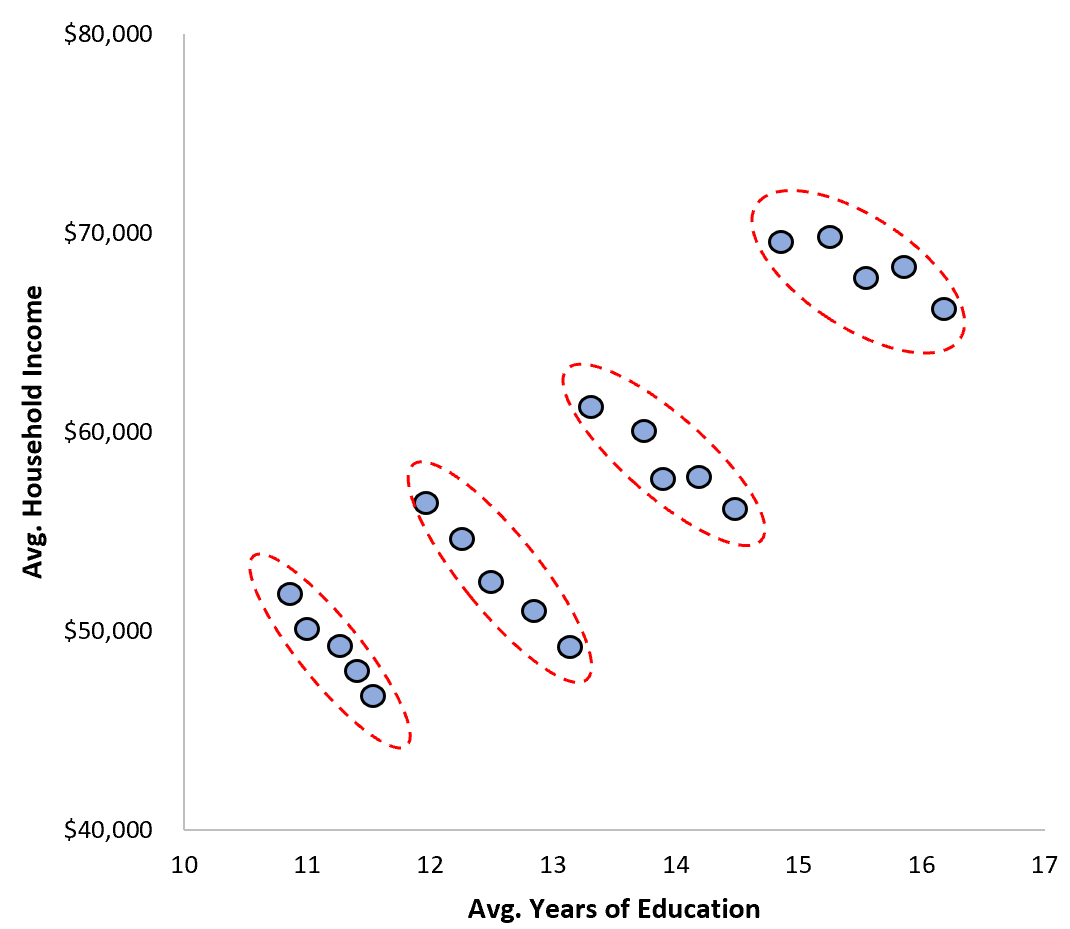
聚合偏差的影响

研究中经常出现聚合偏差，因为人们常常错误地认为，出现在总体水平上的趋势也必然出现在个体水平上。不幸的是，正如前面的示例所示，情况并非总是如此。

聚合偏差可能导致研究结果得出错误的结论并具有误导性。当涉及变量之间的相关性时，这种类型的偏差尤其有害。

即使两个变量的汇总数据之间的相关性是正相关，两个变量在个体观察水平上的潜在相关性实际上可能是：

• 负相关关系
• 没有相关性
• 正相关

避免此类偏差的方法是使用单个数据点而不是汇总数据点进行研究，以便您可以发现两个变量之间的真实关系。