Kendall 的 tau：定义 + 示例

在统计学中，相关性是指两个变量之间关系的强度和方向。相关系数的值范围为 -1 到 1，其中 -1 表示完全负关系，0 表示没有关系，1 表示完全正关系。

最常用的相关系数是皮尔逊相关系数，它衡量两个数值变量之间的线性关联。

不太常用的相关系数是Kendall 的 Tau ，它衡量两列排名数据之间的关系。

Kendall’s Tau（通常缩写为 τ）的计算公式如下：

τ = (CD) / (C+D)

金子：

C = 匹配对的数量

D = 不一致对的数量

以下示例说明如何使用此公式计算两列排名数据的 Kendall’s Tau 排名相关系数。

计算 Kendall’s Tau 的示例

假设两位篮球教练将 12 名球员从最差到最好排名。下表是各教练给球员分配的排名：

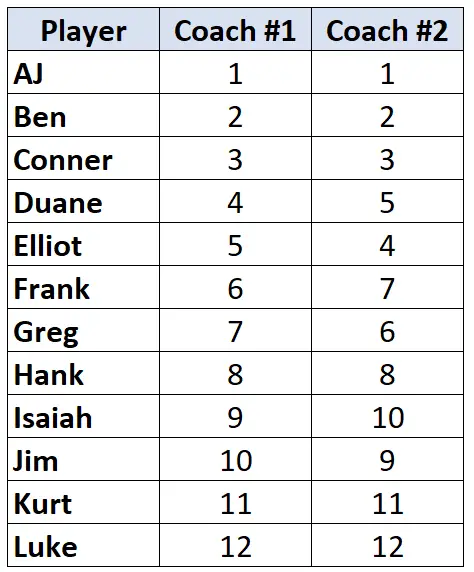
由于我们处理的是两列排名数据，因此使用 Kendall 的 Tau 来计算两位教练排名之间的相关性是合适的。请按照以下步骤计算 Kendall 的 Tau：

步骤1：计算匹配对的数量。

只看教练#2 的排名。从第一个玩家开始，数一下他下面有多少个等级高。例如“1”下面有11个数字较大，所以我们就写11：

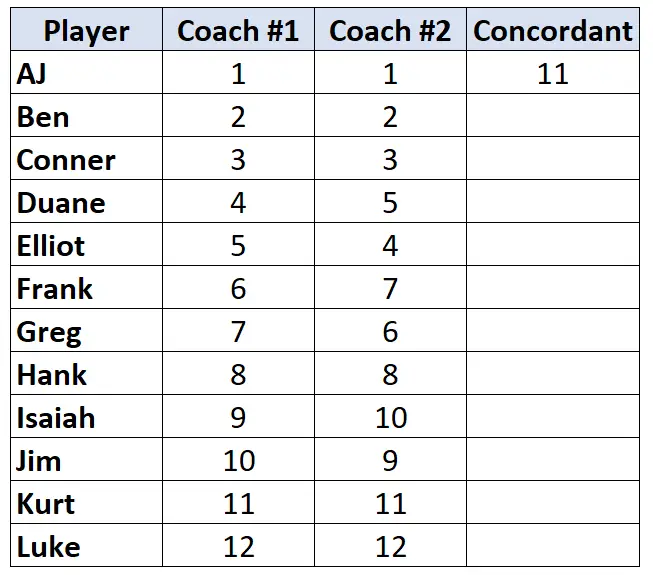
移动到下一个玩家并重复该过程。 “2”下面有 10 个更大的数字，所以我们写 10：

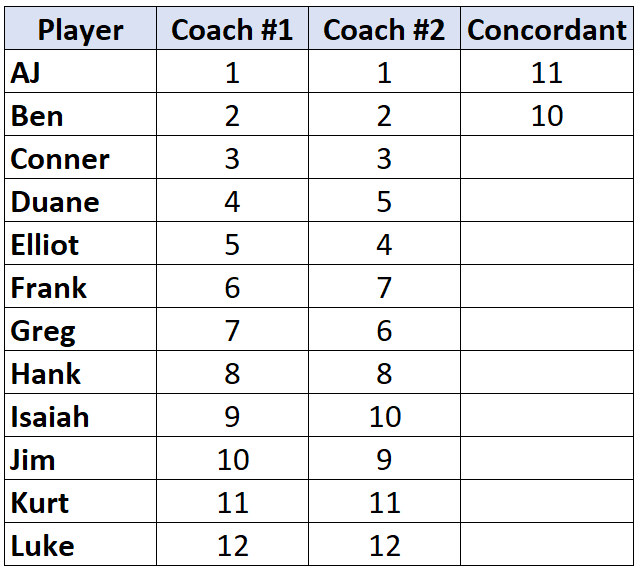
一旦我们找到一个排名低于他之前的玩家的玩家，他就会被简单地分配与他之前的玩家相同的值。例如，埃利奥特的排名为“4”，低于前一个玩家的排名“5”，因此他只是被分配与他之前的玩家相同的值：

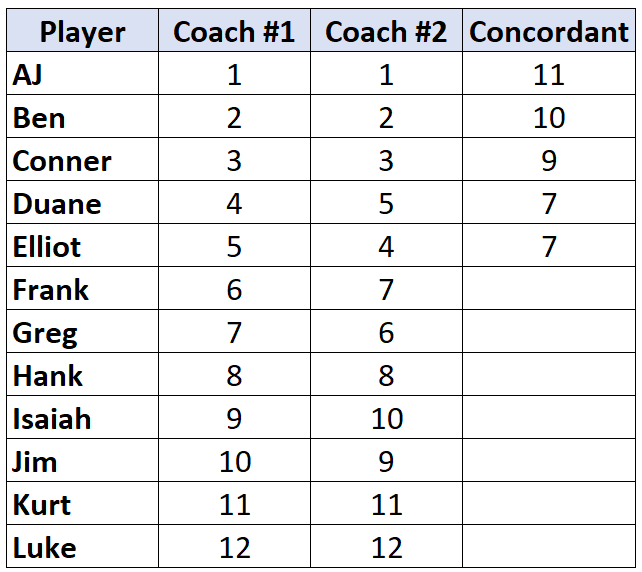
对所有玩家重复此过程：

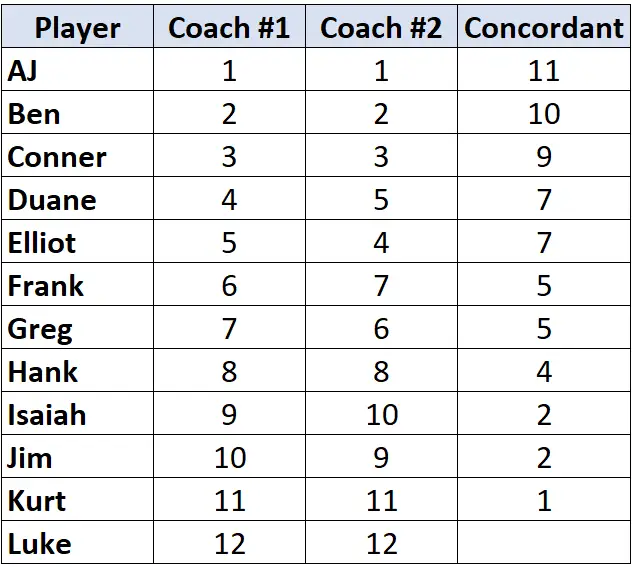
步骤2：计算不一致对的数量。

再次强调，只看教练 #2 的排名。对于每个玩家，计算他或她下面有多少个等级较小。例如，2 号教练为 AJ 分配了排名“1”，并且在他之下的球员没有更低的排名。因此，我们将其赋值为 0：

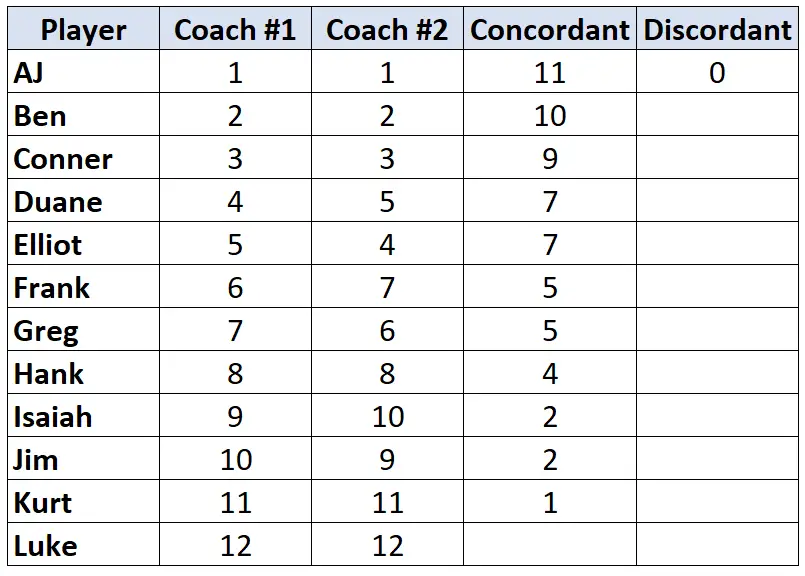
对每个玩家重复此过程：

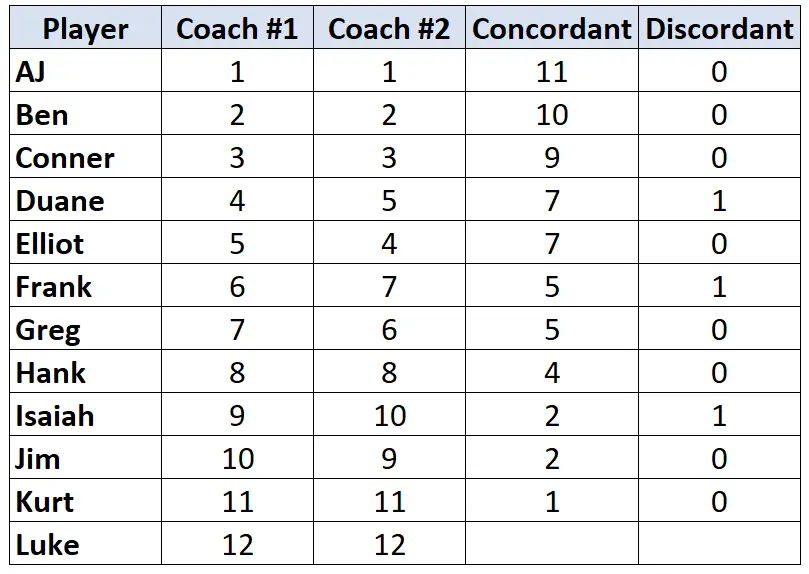
步骤 3：计算每列的总和并找到 Kendall 的 Tau。

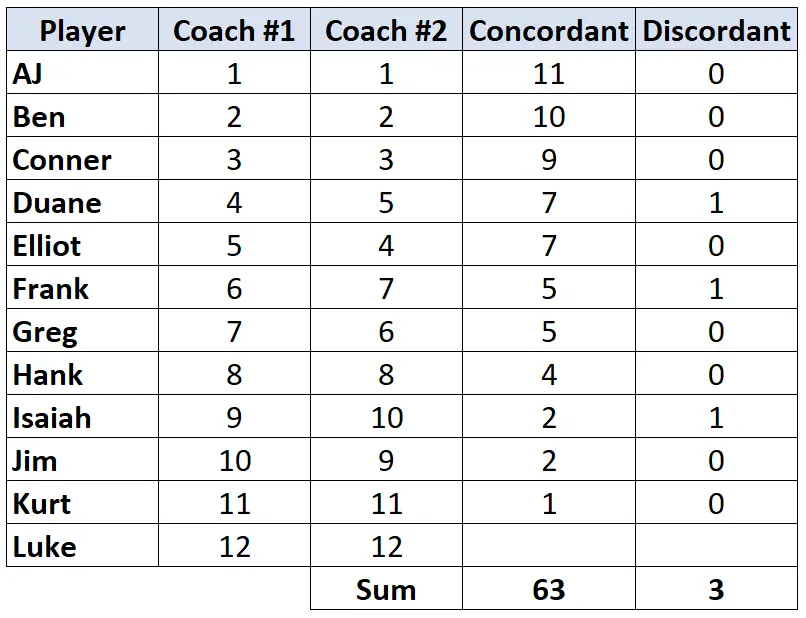
肯德尔的 Tau = (CD) / (C+D) = (63-3) / (63+3) = (60/66) = 0.909 。

Kendall’s Tau 的统计重要性

当 n=10 对以上时，Kendall 的 Tau 通常遵循正态分布。您可以使用以下公式计算 Kendall’s Tau 的 z 分数：

z = 3τ*√ n(n-1) / √ 2(2n+5)

金子：

τ = 您为 Kendall 的 Tau 计算的值

n = 对数

以下是计算上一个示例的z的方法：

z = 3(.909)*√ 12(12-1) / √ 2(2*12+5) = 4.11 。

使用 P 值 Z 得分计算器，我们看到该 z 得分的 p 值为0.00004 ，这在 0.05 alpha 水平上具有统计显着性。因此，两位教练分配给球员的排名之间存在统计上显着的相关性。

附赠：如何在 R 中计算 Kendall 的 Tau

在 R 统计软件中，您可以使用 VGAM 库中的kendall.tau()函数来计算两个向量的 Kendall’s Tau，其语法如下：

肯德尔.tau(x, y)

其中x和y是两个长度相等的数字向量。

以下代码说明了如何计算我们在上一个示例中使用的确切数据的 Kendall’s Tau：

 #load VGAM
library(VGAM)

#create vector for each coach's rankings
coach_1 <- c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12)
coach_2 <- c(1, 2, 3, 5, 4, 7, 6, 8, 10, 9, 11, 12)

#calculate Kendall's Tau
kendall.tau(coach_1, coach_2)

#[1] 0.9090909

请注意 Kendall 的 Tau 值与我们手动计算的值如何匹配。