什么是范围限制？

在统计学中，我们通常寻求测量两个变量之间的相关性。这有助于我们理解以下内容：

• 两个变量之间关系的方向。当一个变量增加时，另一个变量会增加还是减少？
• 两个变量之间关系的强度。两个变量的值变化了多少？

不幸的是，在测量两个变量之间的相关性时可能出现的问题称为范围限制。当其中一个变量的测量值范围由于某种原因受到限制时，就会发生这种情况。

例如，假设我们想要测量特定学校学生的学习时间和考试成绩之间的相关性。

如果我们收集学校所有 1,000 名学生的这两个变量的数据，我们可能会发现学习时间和考试成绩之间的相关性为0.73 。

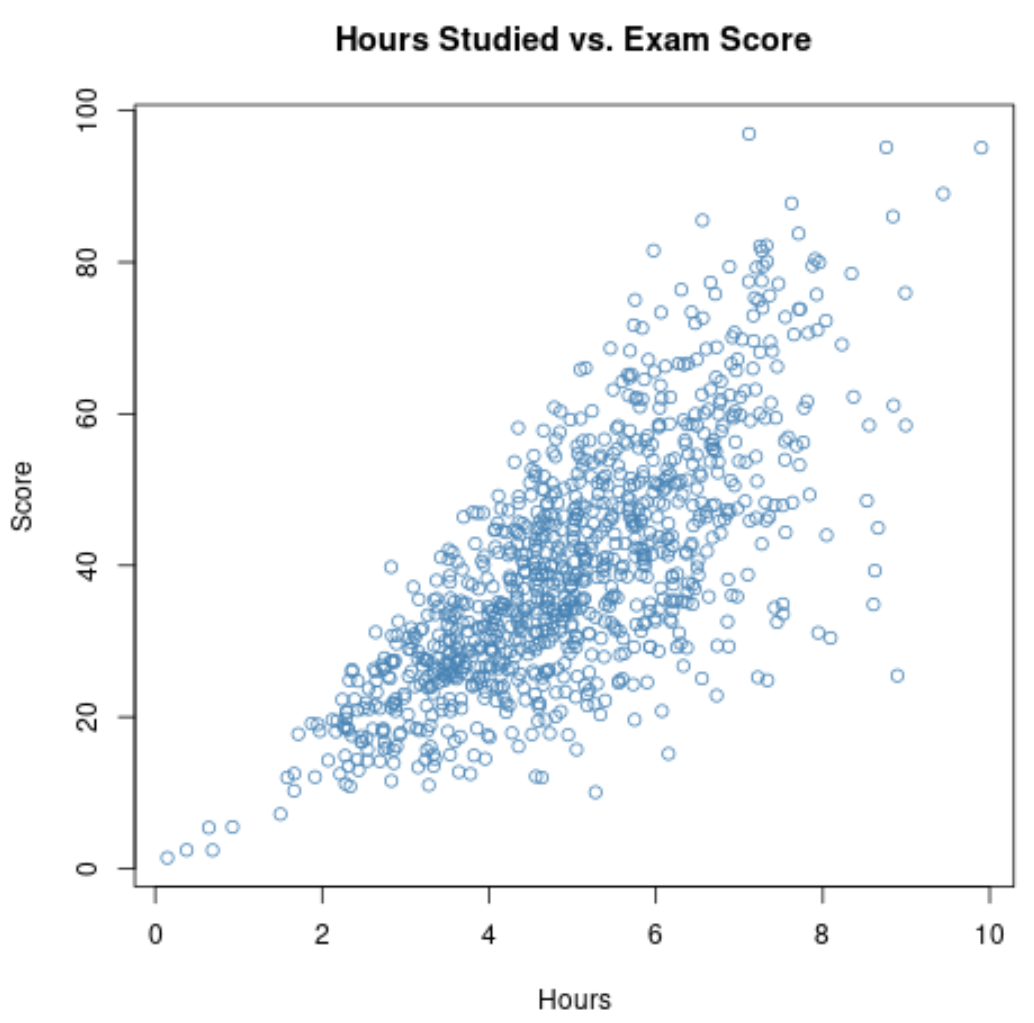
这种相关性相当高，表明两个变量之间存在很强的正相关关系。随着学生学习的越多，他们在考试中往往会表现得更好。

但是，假设我们只收集荣誉课程学生的数据。可能所有这些学生都学习了至少 6 个小时。

因此，如果我们计算这些学生的学习时间和考试成绩之间的相关性，我们将使用一个狭窄的范围来表示学习时间变量。

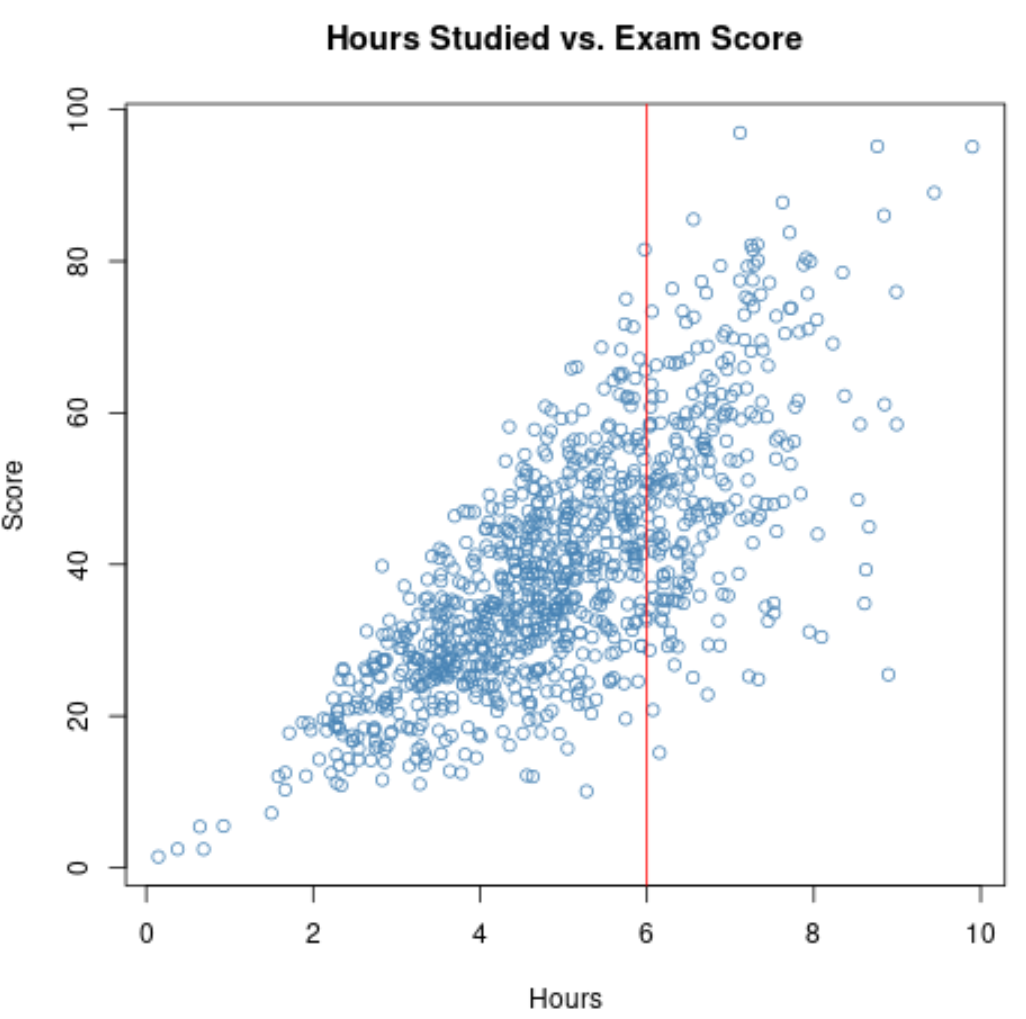
如果我们放大时间大于 6 的范围的散点图，则该图如下所示：

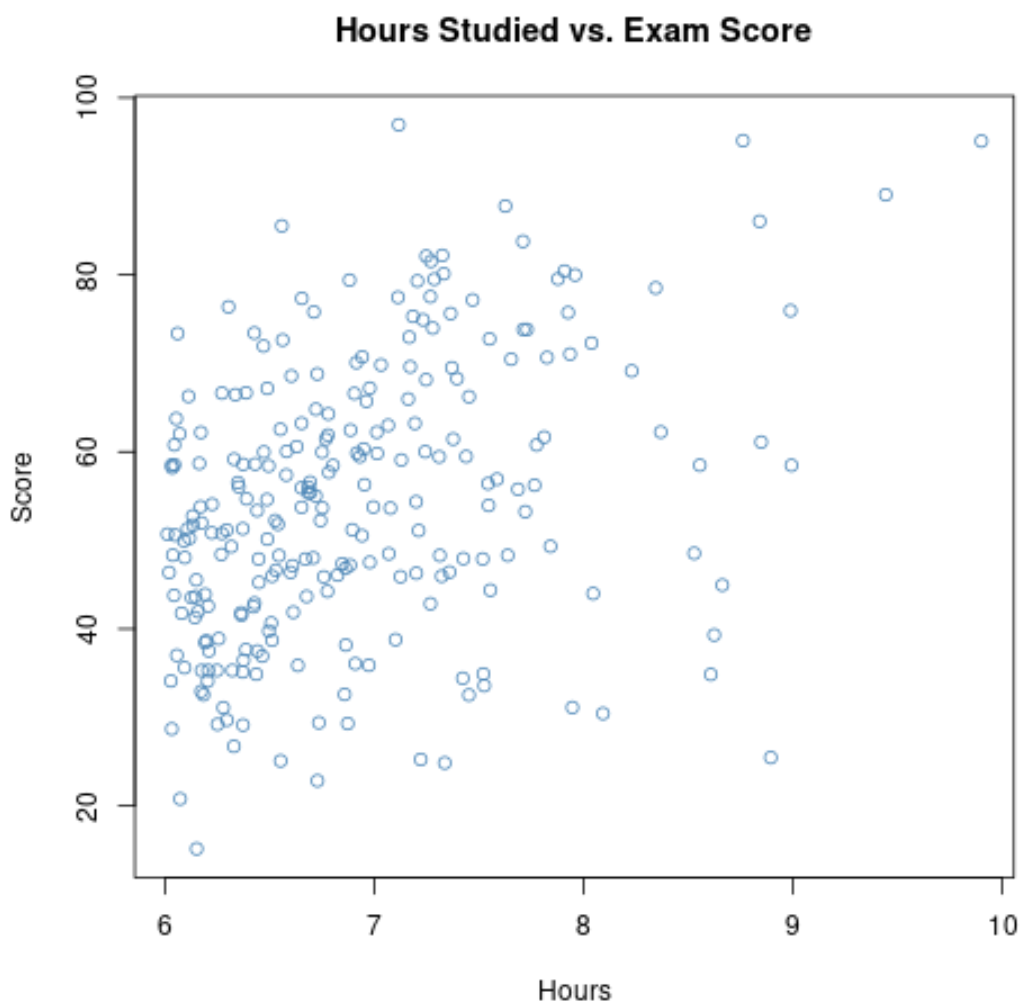
该图上两个变量之间的相关性为0.37 ，明显低于0.73 。

因此，如果我们只收集荣誉课程学生的学习时间和考试成绩数据，我们可能会假设学习时间和考试成绩之间存在弱关系。

然而，这个结果可能会产生误导，因为我们对其中一个变量使用了有限的范围。

限制范围的现实示例

在许多不同的研究实践中，可能会出现限制范围的问题。这里有些例子：

1.高水平运动员研究。研究人员可能有兴趣研究特定的训练计划是否比特定的标准计划产生更多的肌肉质量。

如果研究人员只收集精英运动员的数据，那么这些运动员很可能都已经拥有很高的肌肉质量。因此，可用于计算训练计划和产生的肌肉质量之间的相关性的值范围很窄。

2.优秀学生的研究。研究人员可能想研究某个辅导计划是否对成绩有积极影响。本质上，渴望提高成绩并参加辅导项目的学生可能已经是成绩优异的学生了。

所以这些学生的成绩可能没有太大的提升空间。当研究人员计算辅导项目花费的时间与由此产生的成绩提高之间的相关性时，真正的相关性可能会被低估，因为成绩提高的空间受到了限制。

如何考虑限制范围

解释限制范围的一种流行方法称为“桑代克案例 2” ，该公式由心理测量学家罗伯特·桑代克 (Robert L. Thorndike) 开发。

该公式提供了两个变量之间真实相关性的估计，并使用以下计算：

真实相关性 = √(1-(SD ² _{y 限制}-SD ² _{y 无限制})) * (1-r ²_限制)

金子：

• SD ²_{限制 y} ：响应变量 y 的可用数据的平方标准差。
• _无限制SD ² y：总体响应变量的已知平方标准差。
• r ²_受限：可用受限数据的二次相关。

当其中一个变量受到范围限制时，该公式已被证明可以有效地对两个变量之间的真实相关性进行无偏估计。

请注意，要使用此公式，您必须估计响应变量的真实总体标准差。