集中趋势的度量:定义和示例
集中趋势的度量是代表数据集中心点的单个值。该值也可以称为数据集的“中心位置”。
在统计学中,集中趋势的常用度量有以下三种:
- 平均
- 中位数
- 时尚
这些措施中的每一个都使用不同的方法来查找数据集的中心位置。根据您正在分析的数据类型,使用这三个指标之一可能比其他两个更好。
在本文中,我们将了解如何计算集中趋势的三个度量中的每一个,以及如何根据您的数据确定最适合使用哪个度量。
为什么集中趋势度量有用?
在我们了解如何计算均值、中位数和众数之前,首先了解一下为什么这些测量值实际上很有用是很有帮助的。
考虑以下场景:
一对年轻夫妇正在考虑在新城市的哪里购买他们的第一套房子,他们最多可以花 15 万美元。城市的一些地区有昂贵的房屋,一些地区有便宜的房屋,还有一些地区有中等价格的房屋。他们希望轻松地将搜索范围缩小到适合其预算的特定社区。
如果这对夫妇只查看每个社区的单户住宅价格,他们可能很难确定哪些社区最适合他们的预算,因为他们可能会看到这样的情况:
A区房价: $140,000、$190,000、$265,000、$115,000、$270,000、$240,000、$250,000、$180,000、$160,000、$200,000、$240,000、$280,000……
B区房价: $140,000、$290,000、$155,000、$165,000、$280,000、$220,000、$155,000、$185,000、$160,000、$200,000、$190,000、$140,000、$145.0 0 0,…
C区房价: $140,000、$130,000、$165,000、$115,000、$170,000、$100,000、$150,000、$180,000、$190,000、$120,000、$110,000、$130,000、$120,0 0 0,…
然而,如果他们知道每个社区的房屋平均价格(例如集中趋势的衡量标准),那么他们可以更快地完善搜索,因为他们可以更轻松地识别哪个社区的房价符合他们的预算:
A区房屋均价: $220,000
B区房屋平均价格: $190,000
C区房屋平均价格: $140,000
通过了解每个社区的平均房价,他们可以很快发现社区C可能在其预算范围内拥有最多的可用房屋。
这就是使用集中趋势度量的好处:它可以帮助您了解数据集的中心值,该中心值往往描述数据值通常位于何处。在这个特定的示例中,它可以帮助这对年轻夫妇了解每个社区的房屋典型价格。
要点:集中趋势的度量很有用,因为它为我们提供了描述数据集“中心”的单个值。这有助于我们比仅仅查看数据集中的所有单个值更快地理解数据集。
意思是
最常用的集中趋势度量是平均值。要计算数据集的平均值,只需将所有单个值相加并除以值总数即可。
平均值 =(所有值的总和)/(值的总数)
例如,假设我们有以下数据集,显示同一球队的 10 名棒球运动员在一个赛季中击出的本垒打数量:
| 玩家 | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #十 |
|---|---|---|---|---|---|---|---|---|---|---|
| 本垒打 | 8 | 15 | 22 | 21 | 12 | 9 | 11 | 27 | 14 | 13 |
每个球员的平均本垒打数可以计算如下:
平均值 = (8+15+22+21+12+9+11+27+14+13) / 10 = 15.2圈。
中位数
中位数是数据集的中间值。您可以通过将数据集中的所有单个值从小到大排序并找到中值来找到中位数。如果有奇数个值,则中位数是中间的值。如果有偶数个值,则中位数是中间两个值的平均值。
例如,要查找上例中 10 名棒球运动员击中本垒打的中位数,我们可以按照击中本垒打数的降序对球员进行排名:
| 玩家 | #1 | #6 | #7 | #5 | #十 | #9 | #2 | #4 | #3 | #8 |
|---|---|---|---|---|---|---|---|---|---|---|
| 本垒打 | 8 | 9 | 11 | 12 | 13 | 14 | 15 | 21 | 22 | 27 |
由于我们有偶数个值,因此中位数只是两个中间值的平均值: 13.5 。
相反,考虑一下我们是否有九名玩家:
| 玩家 | #1 | #6 | #7 | #5 | #9 | #2 | #4 | #3 | #8 |
|---|---|---|---|---|---|---|---|---|---|
| 本垒打 | 8 | 9 | 11 | 12 | 14 | 15 | 21 | 22 | 27 |
在本例中,由于我们有奇数个值,因此中位数就是中间的值: 14 。
时尚
众数是数据集中最常出现的值。一个数据集可以没有模式(如果没有值重复)、一种模式或多种模式。
例如,以下数据集没有众数:
| 玩家 | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #十 |
|---|---|---|---|---|---|---|---|---|---|---|
| 本垒打 | 8 | 9 | 11 | 12 | 13 | 14 | 15 | 21 | 22 | 27 |
以下数据集的众数为: 15 。这是最常出现的值。
| 玩家 | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #十 |
|---|---|---|---|---|---|---|---|---|---|---|
| 本垒打 | 8 | 9 | 11 | 12 | 13 | 15 | 15 | 21 | 22 | 27 |
以下数据集具有三种模式: 8、15、19 。这些是最常出现的值。
| 玩家 | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #十 |
|---|---|---|---|---|---|---|---|---|---|---|
| 本垒打 | 8 | 8 | 11 | 12 | 15 | 15 | 17 号 | 19 | 19 | 27 |
在处理分类数据时,众数是衡量集中趋势的特别有用的方法,因为它告诉我们哪个类别出现最频繁。例如,请考虑以下条形图,它显示了有关人们最喜欢的颜色的调查结果:
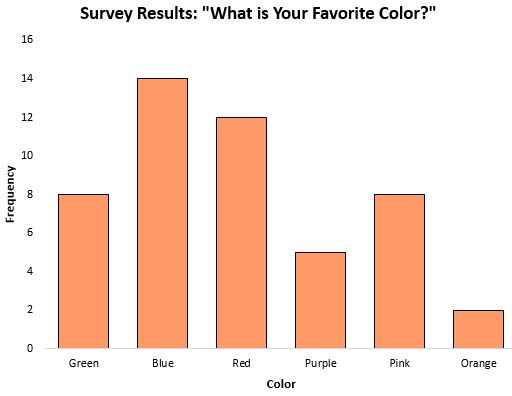
模式,或者说最常出现的响应,是蓝色的。
在数据是分类的情况下(如上面的数据),甚至不可能计算中位数或均值,因此众数是我们可以使用的唯一衡量集中趋势的方法。
该模式也可用于数值数据,正如我们在上面的棒球运动员示例中看到的那样。然而,众数对于回答“这个数据集的典型值是多少?”这个问题往往不太有用。 »
例如,假设我们想知道该队棒球运动员的典型本垒打数:
| 玩家 | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #十 |
|---|---|---|---|---|---|---|---|---|---|---|
| 本垒打 | 8 | 8 | 11 | 12 | 15 | 15 | 17 号 | 19 | 19 | 27 |
该数据集的众数为 8、15 和 19,因为这些是最常见的值。然而,这些对于了解球队中球员的典型本垒打数量并没有多大帮助。在这种情况下,更好的集中趋势衡量标准是中位数 (15) 或平均值(也是 15)。
当众数与其他值相差甚远时,众数也不能很好地衡量集中趋势。例如,以下数据集的众数为 30,但这实际上并不代表球队中每个球员的“典型”本垒打数:
| 玩家 | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #十 |
|---|---|---|---|---|---|---|---|---|---|---|
| 本垒打 | 5 | 6 | 7 | 十 | 11 | 12 | 13 | 15 | 30 | 30 |
同样,平均值或中位数可以更好地描述该数据集的中心位置。
何时使用均值、中位数和众数
我们已经看到,平均值、中位数和众数都以非常不同的方式测量数据集的中心位置或“典型值”:
平均值:查找数据集中的平均值。
中位数:查找数据集中的中值。
众数:查找数据集中最常见的值。
以下是某些集中趋势指标比其他指标更适合使用的场景:
何时使用平均值
当数据分布相当对称并且没有异常值时,最好使用平均值。
例如,假设我们有以下分布,显示某个城市中个人的工资:

由于该分布相当对称(即,如果将其分成两半,则每一半看起来大致相等)并且没有异常值(即(例如没有极高的薪水)),因此平均值可以很好地描述该数据集。
平均值为 63,000 美元,大致位于分布的中心:

何时使用中位数
当数据分布倾斜或存在异常值时,最好使用中位数。
有偏差的数据:
当分布倾斜时,中位数仍然能够捕获中心位置。例如,考虑以下某个城市的个人工资分布:

中位数比平均值更能反映个人的“典型”工资。这是因为分布尾部的大值往往会使均值远离中心并向长尾移动。
在这个特定的例子中,平均值告诉我们,这个城市的典型个人年收入约为 47,000 美元,而中位数告诉我们,典型个人年收入约为 32,000 美元,这更能代表典型个人。
异常值:
当数据中存在异常值时,中位数还有助于更好地捕获分布的中心位置。例如,请考虑下图,该图显示了某条街道上房屋的平方英尺:

平均值很大程度上受到一些非常大的房屋的影响,而中位数则不然。因此,中位数比平均值更能捕捉该街道上房屋的“典型”平方英尺。
何时使用模式
当您处理分类数据并想知道哪个类别出现最频繁时,最好使用此模式。这里有些例子:
- 您正在对人们最喜欢的颜色进行调查,并想知道哪种颜色在回复中出现最频繁。
- 您正在调查人们对三种网站设计选择的偏好,并想知道人们最喜欢哪种设计。
如前所述,如果您使用分类数据,甚至无法计算中位数或均值,这使得众数成为集中趋势的唯一度量。
一般来说,如果您正在处理诸如房屋平方英尺、每个球员击出的本垒打数量、每个人的工资等数值数据,通常最好使用中位数或平均值来描述“典型”值数据集。
注意:需要注意的是,如果数据集完全服从正态分布,则均值、中位数和众数都具有相同的值。