如何解释对数似然值（附示例）

回归模型的对数似然值是衡量模型拟合优度的一种方法。对数似然值越高，模型越适合数据集。

给定模型的对数似然值的范围可以从负无穷到正无穷。给定模型的实际对数似然值通常没有意义，但对于比较两个或多个模型很有用。

在实践中，我们经常将多个回归模型拟合到一个数据集，并选择对数似然值最高的模型作为最适合数据的模型。

以下示例展示了如何在实践中解释不同回归模型的对数似然值。

示例：解释对数似然值

假设我们有以下数据集，显示特定社区中 20 套不同房屋的卧室数量、浴室数量和销售价格：

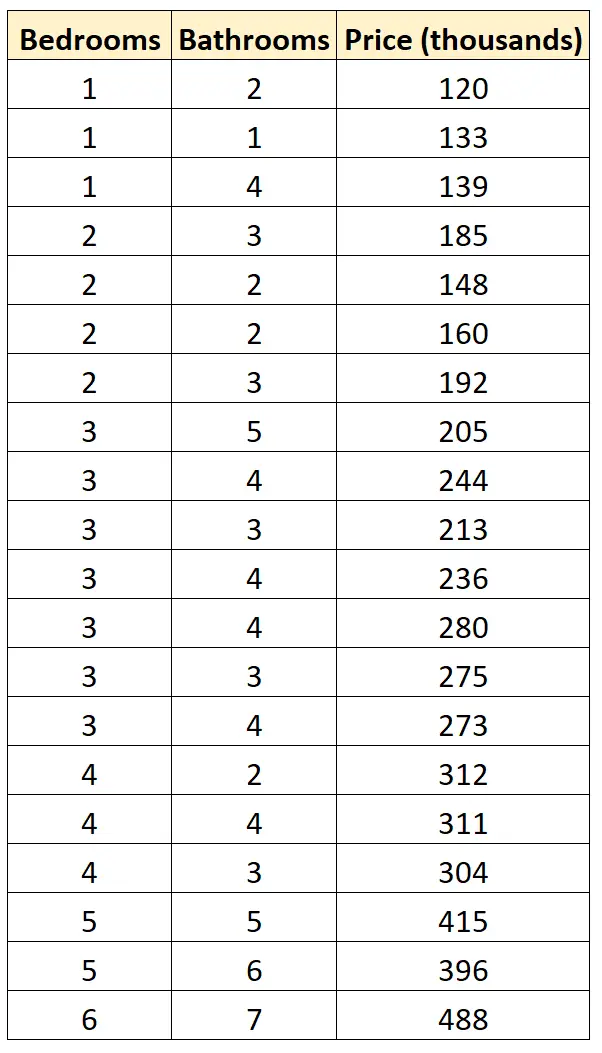
假设我们想要拟合以下两个回归模型并确定哪个模型最适合数据：

模型1 ：价格= _β0 + _β1 （房间数）

模型2 ：价格= _β0 + _β1 （浴室数量）

以下代码显示了如何在 R 中拟合每个回归模型并计算每个模型的对数似然值：

 #define data
df <- data. frame (beds=c(1, 1, 1, 2, 2, 2, 2, 3, 3, 3,
                        3, 3, 3, 3, 4, 4, 4, 5, 5, 6),
                 baths=c(2, 1, 4, 3, 2, 2, 3, 5, 4, 3,
                         4, 4, 3, 4, 2, 4, 3, 5, 6, 7),
                 price=c(120, 133, 139, 185, 148, 160, 192, 205, 244, 213,
                         236, 280, 275, 273, 312, 311, 304, 415, 396, 488))

#fitmodels
model1 <- lm(price~beds, data=df)
model2 <- lm(price~baths, data=df)

#calculate log-likelihood value of each model
logLik(model1)

'log Lik.' -91.04219 (df=3)

logLik(model2)

'log Lik.' -111.7511 (df=3)

第一个模型的对数似然值 ( -91.04 ) 比第二个模型 ( -111.75 ) 更高，这意味着第一个模型提供了更好的数据拟合。

使用对数似然值的注意事项

计算对数似然值时，请务必注意，向模型添加额外的预测变量几乎总是会增加对数似然值，即使额外的预测变量在统计上不显着。

这意味着，只有当每个模型具有相同数量的预测变量时，您才应该比较两个回归模型之间的对数似然值。

要比较具有不同数量的预测变量的模型，您可以执行似然比检验来比较两个嵌套回归模型的拟合优度。

其他资源

如何使用 lm() 函数拟合 R 中的线性模型
如何在 R 中执行似然比检验