调整后的优势比：定义+示例

在统计学中，优势比告诉我们治疗组中事件发生的概率与对照组中事件发生的概率之间的比率。

优势比最常出现在逻辑回归中，这是一种我们用来拟合具有一个或多个预测变量和二元响应变量的回归模型的方法。

调整后的优势比是针对模型中的其他预测变量进行调整的优势比。

在调整其他预测变量的影响后，它对于帮助我们了解预测变量如何影响事件发生的机会特别有用。

以下示例说明了优势比和调整后的优势比之间的差异。

示例：调整后优势比的计算

假设我们想了解母亲的年龄是否会影响生出低出生体重婴儿的可能性。

为了探索这一点，我们可以使用年龄作为预测变量，使用低出生体重（是或否）作为响应变量来执行逻辑回归。

假设我们收集 300 名母亲的数据并拟合逻辑回归模型。结果如下：

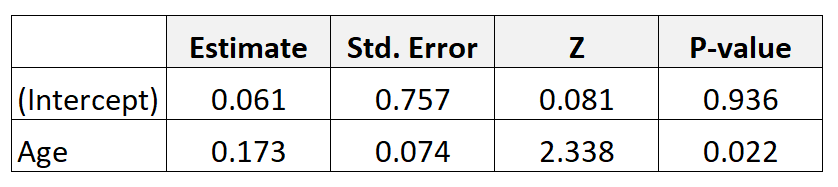
要获得年龄的优势比，只需对表中的系数估计值取幂即可： e ^0.173 = 1.189 。

这告诉我们，年龄增加一岁，婴儿出生体重过轻的几率就会增加1,189 。换句话说，年龄每增加一年，低出生体重婴儿的几率就会增加18.9% 。

该优势比称为“粗略”优势比或“未调整”优势比，因为它是模型中唯一的预测变量，因此尚未针对模型中的其他预测变量进行调整。

但假设我们想了解母亲的年龄和吸烟习惯是否会影响生出低出生体重婴儿的可能性。

为了探索这一点，我们可以使用年龄和吸烟（是或否）作为预测变量，并使用低出生体重作为响应变量来执行逻辑回归。

假设我们收集 300 名母亲的数据并拟合逻辑回归模型。结果如下：

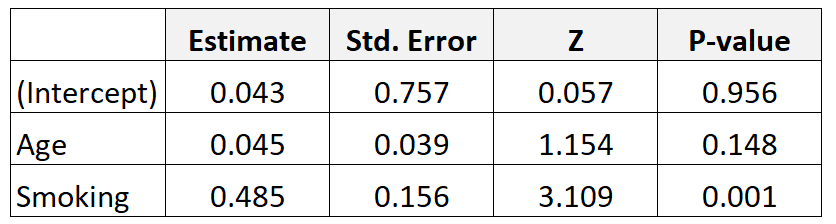
以下是如何解释结果：

年龄：年龄调整优势比计算如下：e ^0.045 = 1.046 。这意味着，假设吸烟变量保持不变，年龄每增加一年，出生体重低的婴儿的几率就会增加 4.6%。

例如，假设母亲 A 和母亲 B 都吸烟。如果母亲A比母亲B大一岁，那么母亲A生出低出生体重婴儿的概率是母亲B生出低出生体重婴儿的概率的1.046倍。

吸烟：调整后的吸烟优势比计算如下： ^e.485 = 1.624 。这意味着，假设年龄变量保持不变，如果母亲吸烟（与不吸烟相比），生出低出生体重婴儿的几率会增加 62.4%。

例如，假设母亲 A 和母亲 B 都是 30 岁。如果母亲A在怀孕期间吸烟，而母亲B不吸烟，那么母亲A生出低体重儿的几率比母亲B生出低体重儿的几率高62.4%。

请注意，年龄调整后的优势比低于上一示例中未调整的优势比。这是因为当其他预测变量增加响应变量发生的机会时，模型中已存在的预测变量的调整优势比将始终降低。

摘要：优势比与调整后的优势比

优势比（有时称为“粗”优势比）有助于告诉我们预测变量的变化如何影响响应变量发生的机会。

在控制模型中的其他预测变量后，调整后的优势比有助于告诉我们预测变量的变化如何影响响应变量发生的机会。

其他资源

逻辑回归简介
如何在 R 中执行逻辑回归
如何在 Python 中执行逻辑回归