贝叶斯定理

经过 8月 1, 2023 可能性 0 条评论

本文解释了什么是贝叶斯定理以及它在概率和统计中的用途。因此，您将了解贝叶斯定理的公式是什么、贝叶斯定理的解决示例以及该定理的应用是什么。

什么是贝叶斯定理？

在概率论中，贝叶斯定理是用于在已知事件的先验信息时计算该事件的概率的定律。

更具体地说，贝叶斯定理在数学上将给定事件 B 的事件 A 的概率与给定 A 的事件 B 的概率联系起来。

例如，如果您事先知道一个人在患流感时会头痛的概率，则可以使用贝叶斯定理来确定一个人在头痛时患流感的概率。

贝叶斯定理有很多应用，例如，它在医学、经济学或技术中用于计算受其他事件制约的某些事件的概率。下面，我们将详细介绍贝叶斯定理的不同应用。

贝叶斯定理是由英国数学家托马斯·贝叶斯（Thomas Bayes，1702-1761）发明的，尽管该定理是在他去世后于 1763 年出版的。

➤请参阅：条件概率

贝叶斯定理的公式

贝叶斯定理指出，给定一个由一组概率不为零的互斥事件{A 1 , A 2 ,…, A i ,…, A n } 和另一个事件 B 组成的样本空间，我们可以在数学上将条件关联起来给定事件 B 时 A i的概率以及给定 A i时 B 的条件概率。

因此，贝叶斯定理，也称为贝叶斯规则，其公式为：

贝叶斯定理的公式、贝叶斯规则

金子：

  • P(A_i|B)

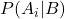
    是事件 A i给定事件 B 的条件概率，称为后验概率。

  • P(B|A_i)

    是给定事件 A i时事件 B 的条件概率。

  • P(A_i)

    是事件 A i发生的概率，称为先验概率。

请注意，贝叶斯定理公式的分母是事件 B 的总概率。

贝叶斯定理示例

一旦我们了解了贝叶斯定理的定义及其公式是什么，我们将看到一个已解决的示例，说明如何使用贝叶斯定理计算概率，以更好地理解该概念。

  • 一家电子商店销售三个品牌的电视：X、Y、Z。估计销售额的 20% 是有缺陷的品牌电视，3% 的 Y 品牌电视有缺陷，4% 的 Z 品牌电视有缺陷。给定一台有缺陷的电视，它是 Z 品牌电视的概率是多少？

该练习为我们提供了客户购买每个品牌电视的概率：

  • 事件 A 1 ：顾客购买 X 品牌电视 → P(A 1 )=0.20
  • 事件 A 2 ：顾客购买 Y 品牌电视 → P(A 2 )=0.50
  • 事件 A 3 ：顾客购买 Z 品牌电视 → P(A 3 )=0.30

此外，读数还为我们提供了每个品牌的电视有缺陷的概率：

事件B：电视故障

  • B|A 1 ：给定一台品牌 X 电视，该电视有缺陷 → P(B|A 1 )=0.05
  • B|A 2 ：给定一台 Y 品牌电视，该电视有缺陷 → P(B|A 2 )=0.03
  • B|A 3 ：给定一台 Z 品牌电视，该电视有缺陷 → P(B|A 3 )=0.04

所以我们感兴趣的所有事件的概率树如下：

贝叶斯定理树图

因此，要计算给定一台有缺陷的电视机为品牌 Z 的概率，我们必须使用贝叶斯定理中的公式：

P(A_i|B)=\cfrac{P(B|A_i)\cdot P(A_i)}{\displaystyle \sum_{k=1}^n P(B|A_k)\cdot P(A_k)}

使用本例中使用的术语，贝叶斯公式如下所示：

P(A_3|B)=\cfrac{P(B|A_3)\cdot P(A_3)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)+ P(B|A_3)\cdot P(A_3)}

因此，给定的有缺陷电视是品牌 Z 的概率的计算如下：

\begin{aligned}P(A_3|B)&=\cfrac{P(B|A_3)\cdot P(A_3)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)+ P(B|A_3)\cdot P(A_3)}\\[2ex]&=\cfrac{0,04\cdot 0,30}{0,05\cdot 0,20+0,03\cdot 0,50+0,04\cdot 0,30}\\[2ex]&=0,32\end{aligned}

综上所述，如果一台电视机有缺陷，其属于 Z 品牌的概率为 32%。

贝叶斯定理的应用

贝叶斯定理有很多应用，包括：

  1. 医学测试：贝叶斯定理在医学中经常用于确定通过诊断测试的概率。例如，在艾滋病毒检测中，如果检测结果呈阳性，该定理可用于计算一个人实际感染病毒的概率。
  2. 财务分析：在金融领域，贝叶斯定理用于计算在给定一组经济变量的情况下发生某些经济事件（例如股票价值增加或减少）的概率。
  3. 市场研究：贝叶斯定理可以确定，例如，一个人在看到该产品的广告后购买该产品的概率。
  4. 天气预报：天气模型还使用贝叶斯定理来确定基于观测数据的给定天气预报实现的概率。这提高了气候预报的准确性。
  5. 计算机安全– 在网络安全中，可以应用贝叶斯定理来确定可疑活动确实是对计算机系统的攻击的可能性。

解决贝叶斯定理问题

练习1

据估计，1%的人口患有某种疾病。检测这种疾病的测试对于阳性病例的准确率是 95%，对于阴性病例的准确率是 90%。如果随机选择的一个人检测呈阳性，他们实际上患有这种疾病的概率是多少？

练习陈述给了我们以下概率：

A 1 : 该人患有疾病 → P(A 1 )=0.01
A 2 : 该人没有患病 → P(A 2 )=0.99

B：检测结果呈阳性
B|A 1 ：当该人患有疾病时测试呈阳性 → P(B|A 1 )=0.95
B|A 2 ：当该人没有患病时，测试结果为阳性 → P(B|A 2 )=1-0.90=0.10

然后，为了计算随机选择的人在检测呈阳性时实际患有该疾病的概率，必须应用贝叶斯规则：

P(A_i|B)=\cfrac{P(B|A_i)\cdot P(A_i)}{\displaystyle \sum_{k=1}^n P(B|A_k)\cdot P(A_k)}

P(A_1|B)=\cfrac{P(B|A_1)\cdot P(A_1)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)}

所以我们将这些值代入公式并进行概率计算：

\begin{aligned}P(A_1|B)&=\cfrac{P(B|A_1)\cdot P(A_1)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)}\\[2ex]&=\cfrac{0,95\cdot 0,01}{0,95\cdot 0,01+0,10\cdot 0,99}\\[2ex]&=0,0876\end{aligned}

简而言之，随机选择的一个人检测呈阳性且实际患有该疾病的概率为 8.76%。

练习2

据估计，一只股票一天内上涨的概率为40%，保持稳定的概率为10%，下跌的概率为50%。此外，我们知道，当市场上涨时，金融分析师预测正确的概率为 90%，当市场保持稳定时，预测正确的概率为 75%，而当市场下跌时，正确预测的概率为 75%。 85%.%。如果分析师预测市场将下跌，那么实际下跌的可能性有多大？

在这种情况下，练习语句为我们提供了以下概率：

A 1 : 一日行情上涨 → P(A 1 )=0.40
A 2 : 市场在一天内保持稳定 → P(A 2 )=0.10
A 3 : 一日行情上涨 → P(A 3 )=0.50

B：分析师预测市场将会下跌
B|A 1 ：分析师正确预测市场将会上涨 → P(B|A 1 )=0.90
B|A 2 ：分析师正确预测市场保持稳定 → P(B|A 2 )=0.75
B|A 3 ：分析师正确预测市场将下跌 → P(B|A 3 )=0.85

为了确定分析师预测市场将下跌并且预测正确的概率，我们需要使用贝叶斯定理公式：

P(A_i|B)=\cfrac{P(B|A_i)\cdot P(A_i)}{\displaystyle \sum_{k=1}^n P(B|A_k)\cdot P(A_k)}

P(A_3|B)=\cfrac{P(B|A_3)\cdot P(A_3)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)+ P(B|A_3)\cdot P(A_3)}

我们将概率值代入贝叶斯公式并计算概率：

\begin{aligned}P(A_3|B)&=\cfrac{P(B|A_3)\cdot P(A_3)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)+ P(B|A_3)\cdot P(A_3)}\\[2ex]&=\cfrac{0,85\cdot 0,50}{0,90\cdot 0,40+0,75\cdot 0,10+0,85\cdot 0,50}\\[2ex]&=0,4942\end{aligned}

因此，分析师预测股市将下跌的正确概率为 49.42%。

关于作者

安德森博
本杰明·安德森博

大家好，我是本杰明，一位退休的统计学教授，后来成为 Statorials 的热心教师。 凭借在统计领域的丰富经验和专业知识，我渴望分享我的知识，通过 Statorials 增强学生的能力。了解更多

添加评论

您的电子邮箱地址不会被公开。 必填项已用*标注