超几何分布
在本文中,我们解释什么是超几何分布以及如何使用此类分布计算概率。您可以在线找到超几何分布的公式、其特征是什么,以及计算超几何分布概率的计算器。
什么是超几何分布?
超几何分布是一种概率分布,描述了在不替换总体中的n 个元素的情况下随机提取的成功案例的数量。
也就是说,超几何分布用于计算当从总体中提取n个元素而不替换其中任何一个时获得x次成功的概率。
超几何分布具有三个参数:
- N :总体中元素的数量(N = 0, 1, 2,…)。
- K :是最大成功案例数(K = 0, 1, 2,…,N)。由于在超几何分布中,一个元素只能被视为“成功”或“失败”,因此NK是失败案例的最大数量。
- n :是执行的无替换读取的次数。
![]()
例如,具有参数 N=8、K=5 和 n=3 的超几何分布的离散随机变量 X 定义如下:
![]()
超几何分布公式
超几何分布的公式是K在x上的组合数与NK在nx上的组合数除以N在n上的组合数的乘积。

其中N是人口规模, K是有利事例的总数, n是无放回提取的数量, x是必须计算发生概率的有利事例的数量。
👉您可以使用下面的计算器来计算遵循超几何分布的变量发生事件的概率。
超几何分布示例
了解了超几何分布的定义和公式后,现在我们将逐步解决一个示例,以便您了解如何计算超几何分布的概率。
- 在一个袋子里,我们放了20个蓝球和30个红球,也就是说,袋子里总共有50个球。如果我们抽取 12 个球而不更换任何球,求抽取 4 个蓝色球的概率。
解决这个练习我们需要做的第一件事是确定超几何分布的参数。在这种情况下,总体中的元素总数为 50( N = 50),有利情况的最大数量为 20( K = 20),抽出 12 个球( n = 12)。
![Rendered by QuickLaTeX.com \left.\begin{array}{c}N=50\\[2ex]K=20\\[2ex]n=12\end{array}\right\} \longrightarrow \ X\sim HG(50,20,12)](https://statorials.org/wp-content/ql-cache/quicklatex.com-352132f74408eab99d3985c63a49f322_l3.png)
我们想要计算抽到 4 个蓝色球( x =4)的概率,因此我们应用超几何分布公式,将变量替换为对应的值并进行计算:
![Rendered by QuickLaTeX.com P\bigl[X=x\bigr]=\cfrac{\begin{pmatrix}K\\x\end{pmatrix}\begin{pmatrix}N-K\\n-x\end{pmatrix}}{\begin{pmatrix}N\\n\end{pmatrix}}](https://statorials.org/wp-content/ql-cache/quicklatex.com-caf83b14deae0fe9882e4d40e677329f_l3.png)
![Rendered by QuickLaTeX.com \begin{aligned}P\bigl[X=4\bigr]&=\cfrac{\begin{pmatrix}20\\4\end{pmatrix}\begin{pmatrix}50-20\\12-4\end{pmatrix}}{\begin{pmatrix}50\\12\end{pmatrix}} \\[1.5ex]&=\cfrac{\begin{pmatrix}20\\4\end{pmatrix}\begin{pmatrix}30\\8\end{pmatrix}}{\begin{pmatrix}50\\12\end{pmatrix}} \\[1.5ex]&=0,2336 \end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-ed747dd327149d4a925e6ad7c4119f81_l3.png)
超几何分布计算器
将超几何分布的参数输入以下在线计算器,计算所需事件发生的概率。
请记住, N是总体规模, K是有利案例的总数, n是样本大小, x是我们要查找发生这种情况的概率的值。
超几何分布的特征
超几何分布具有以下性质:
- 超几何分布的期望值等于样本中的元素数量乘以有利案例总数除以总体中的元素数量。
![]()
- 超几何分布的众数是n+1乘以K+1除以N+2 的乘积向下舍入的值。
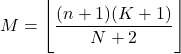
- 超几何分布的方差可以使用以下表达式获得:
![]()
- 超几何分布的矩生成函数如下:
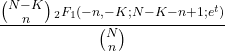
- 超几何分布的特征函数如下:
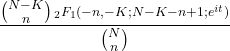
- 给定数量的事件发生的概率可以使用超几何分布的递归根据前一个事件的概率来计算:
![]()
超几何分布和二项分布
超几何分布与二项式分布的区别在于替换。当检索未被替换时,使用超几何分布,但是,在二项式分布中,检索被替换。
例如,如果我们在一副牌中随机抽出五张牌,并且想要计算获得某张牌的概率,如果我们不替换抽出的每张牌,则必须使用超几何分布来进行计算。但是,如果在取出卡片时我们在执行下一次提取之前将其放回去,那么我们必须使用二项式分布来计算概率。
当数量N较大、 n/N比率较小且期望的有利情况数量很少时,我们可以使用超几何分布作为二项式分布的近似。但是,我不推荐它,因为结果不太可靠,而且用二项式定律计算概率比用超几何定律更容易。