辛普森多样性指数：定义与示例

辛普森多样性指数是衡量社区物种多样性的一种方法。

记下D ，该指数计算如下：

D = Σn _i (n _i -1) / N(N-1)

金子：

• n _i :属于物种i的生物体数量
• N：生物总数

辛普森多样性指数的值在0到1之间。值越高，多样性越低。

由于这种解释有些违反直觉，我们经常计算辛普森多样性指数（有时称为优势指数），计算公式为：1 – D。该指数的值越高，物种的多样性越高。

我们还可以计算辛普森指数的倒数，计算公式为 1/D。该指数的最低值为1，最高值为物种数。

例如，如果有7个不同的物种，则该指数的最大值将为7。该指数的值越高，物种多样性越大。

以下分步示例展示了如何计算给定社区的这些不同指数。

第 1 步：收集数据

假设一位生物学家想要测量当地森林的物种多样性。它收集以下数据：

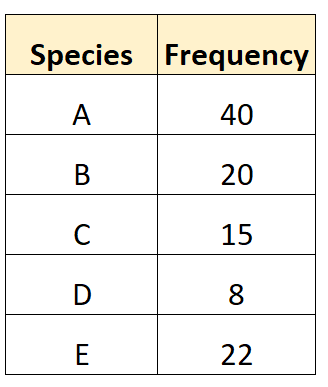
步骤2：计算N

然后她就可以计算出生物体的总数。

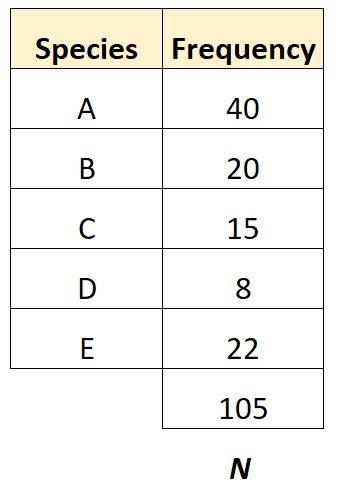
共有105个组织。

步骤3：计算n _i (n _i -1)

然后就可以计算出n _i (n _i -1)。例如，第一个物种的计算如下：40*(40-1) = 1560。她可以对每个物种重复此计算：

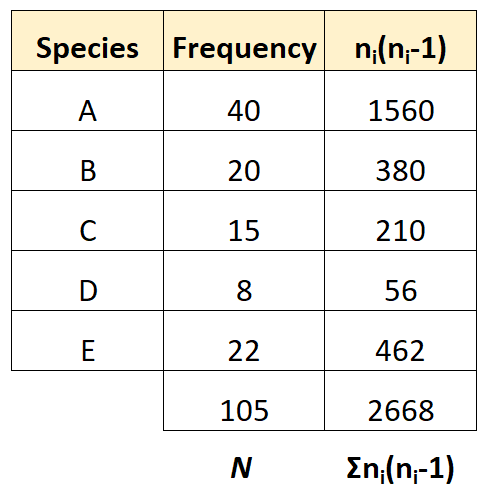
步骤 4：计算辛普森多样性指数

最后，我们可以使用下面的公式来计算辛普森指数：

D = Σn _i (n _i -1) / N(N-1)

使用我们之前找到的值，辛普森指数可以计算如下：

D = 2.668 / (105*(105-1)) = 0.244 。

我们还可以计算辛普森多样性指数如下： 1 – D = 1 – 0.244 = 0.756 。

我们还可以计算辛普森指数的倒数为 1/ D = 1/.244 = 4.09 。

其他资源

请随意使用此辛普森多样性指数计算器来自动计算任何数据集的辛普森多样性指数。