什么是边际平均数？ （定义&#038；示例）

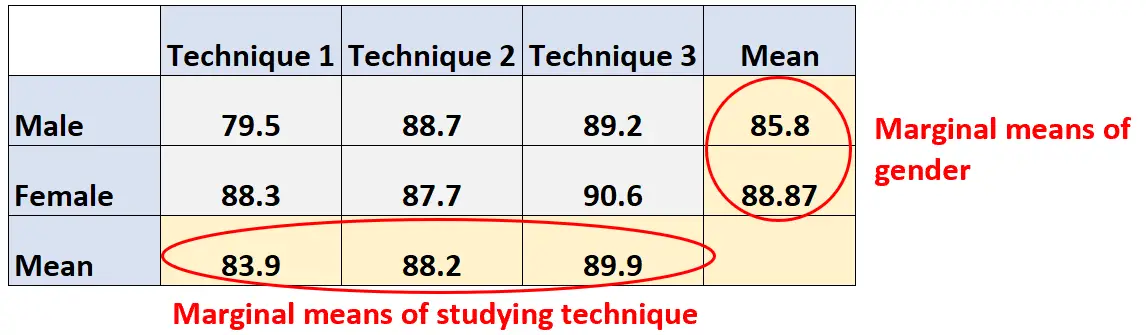
在列联表中，变量的边际均值是该变量在其他变量的每个水平上的平均值。

顾名思义，这些平均值出现在列联表的边缘。

以下示例显示如何计算给定列联表的边际均值。

示例：边际平均值的计算

下面的列联表显示了 100 名学生使用三种不同的学习技巧来准备考试的平均考试成绩。

行显示学生的性别，列显示他们使用的学习技巧：

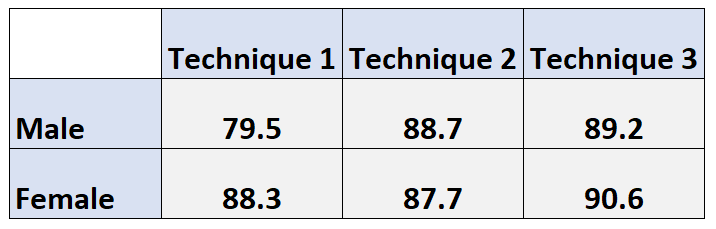
性别边际平均值只是每个学习技术水平的每个性别水平的平均值。

例如，男性的平均边际考试分数计算如下：

男性边际平均值：(79.5 + 88.7 + 89.2) / 3 = 85.8

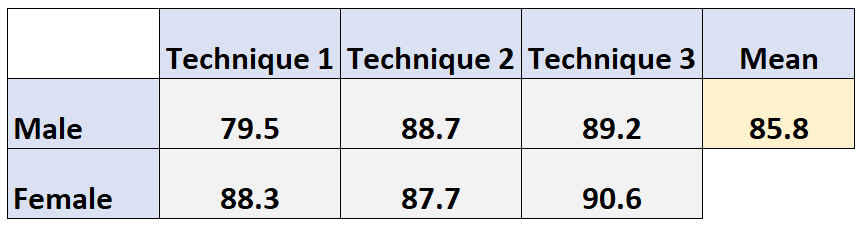
同样，女性的边际平均考试成绩计算如下：

女性边际平均值：(88.3 + 87.7 + 90.6) / 3 = 88.87

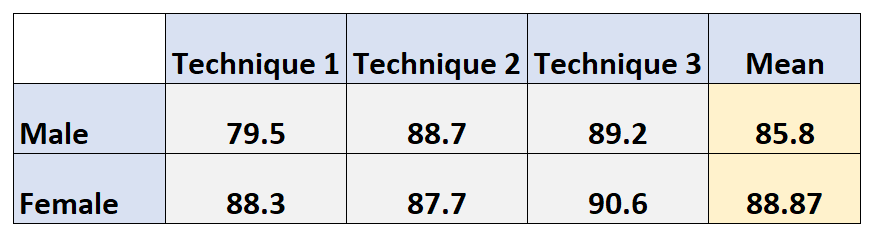
学习技术的边际均值就是每个性别水平的每个学习技术水平的平均值。

例如，使用技术 1 的学生的边际平均考试成绩计算如下：

技术 1 的边际平均值：(79.5 + 88.3) / 2 = 83.9

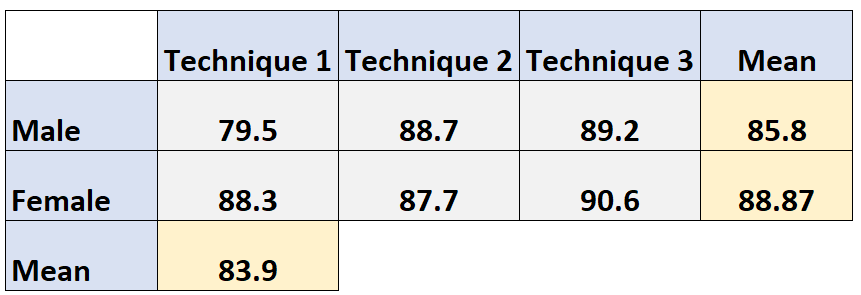
使用技术 2 的学生的边际平均考试成绩计算如下：

技术 2 的边际平均值：(88.7 + 87.7) / 2 = 88.2

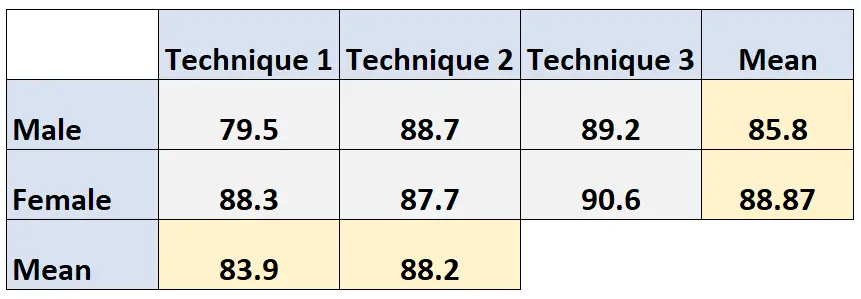
使用技术 3 的学生的边际平均考试成绩计算如下：

技术 3 的边际平均值：(89.2 + 90.6) / 2 = 89.9

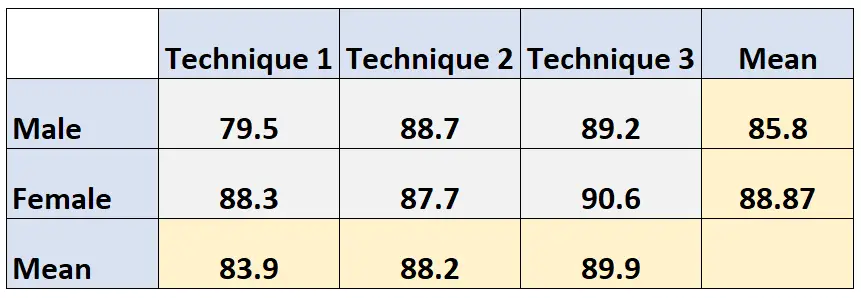
我们可以看到两个变量的边际均值出现在列联表的边际中：

为什么要诉诸边际手段？

边际均值很有用，因为它们告诉我们特定变量水平的总体平均值。

例如，在前面的场景中，我们知道以下内容：

• 使用学习技巧 1 的男性的平均考试成绩为 79.5。
• 使用学习技巧 2 的男性的平均考试成绩为 88.7。
• 使用学习技巧 3 的男性的平均考试成绩为 89.2。

但如果我们只想知道男性的总体平均分怎么办？

男性的边际平均分可以回答这个问题：男性的总体平均分是85.8 。

同样，我们知道以下内容：

• 使用学习技巧 1 的男性的平均考试成绩为 79.5。
• 使用学习技巧 1 的女性的平均考试成绩为 88.3。

但是，如果我们只想知道使用学习技巧 1 的学生的总体平均分怎么办？

学习技巧的边际平均值可以回答这个问题：使用学习技巧 1 的学生的总体平均分是83.9 。

本质上，边际平均值为我们提供了一种简单的方法来理解特定变量水平的平均值。

其他资源

什么是边际分布？
什么是联合分配？
什么是条件分布？