如何检查方差分析假设
单向方差分析是一种统计检验,用于确定三个或更多独立组的平均值之间是否存在显着差异。
以下是我们何时可以使用单向方差分析的示例:
您将一个由 90 名学生组成的班级随机分为三组,每组 30 人。每组使用不同的学习技巧一个月来准备考试。月底,所有学生参加相同的考试。
您想知道学习技巧是否会影响考试成绩。因此,您执行单向方差分析来确定三组的平均分数之间是否存在统计显着差异。
在执行单向方差分析之前,我们必须首先验证是否满足三个假设。
1. 正态性——每个样本都是从正态分布的总体中抽取的。
2. 方差相等——抽取样本的总体方差相等。
3. 独立性——各组内的观察结果彼此独立,并且组内的观察结果是通过随机抽样获得的。
如果不满足这些假设,我们的单向方差分析结果可能不可靠。
在本文中,我们将解释如何检查这些假设以及如果违反其中任何假设该怎么办。
假设#1:常态
方差分析假设每个样本都是从正态分布的总体中抽取的。
如何在 R 中检验这个假设:
为了验证这个假设,我们可以使用两种方法:
- 使用直方图或QQ 图直观地验证假设。
- 使用 Shapiro-Wilk、Kolmogorov-Smironov、Jarque-Barre 或 D’Agostino-Pearson 等正式统计检验验证假设。
例如,假设我们招募 90 人参加一项减肥实验,其中我们随机分配 30 人遵循计划 A、计划 B 或计划 C,为期一个月。为了了解该计划是否对减肥有影响,我们想要进行单向方差分析。以下代码演示了如何使用直方图、QQ 图和 Shapiro-Wilk 检验来检查正态性假设。
1. 拟合方差分析模型。
#make this example reproducible
set.seed(0)
#create data frame
data <- data. frame (program = rep(c(" A ", " B ", " C "), each = 30 ),
weight_loss = c(runif(30, 0, 3),
runif(30, 0, 5),
runif(30, 1, 7)))
#fit the one-way ANOVA model
model <- aov(weight_loss ~ program, data = data)
2. 创建响应值的直方图。
#create histogram
hist(data$weight_loss)
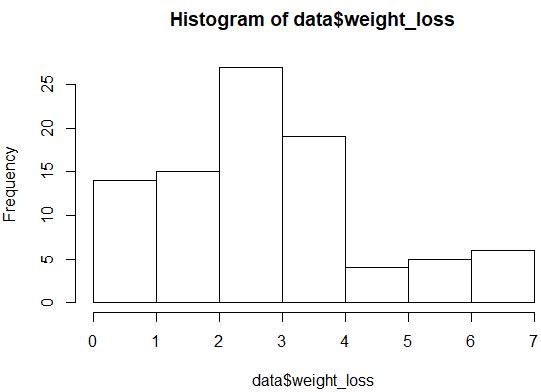
该分布看起来不是很正态分布(例如,它不是“钟形”形状),但我们也可以创建一个 QQ 图来重新观察该分布。
3. 创建残差 QQ 图
#create QQ plot to compare this dataset to a theoretical normal distribution qqnorm(model$residuals) #add straight diagonal line to plot qqline(model$residuals)

一般来说,如果数据点位于 QQ 图中的直线对角线上,则数据集可能服从正态分布。在这种情况下,我们可以看到沿末端的线有明显的偏差,这可能表明数据不呈正态分布。
4. 执行 Shapiro-Wilk 正态性检验。
#Conduct Shapiro-Wilk Test for normality shapiro. test (data$weight_loss) #Shapiro-Wilk normality test # #data: data$weight_loss #W = 0.9587, p-value = 0.005999
Shapiro-Wilk 检验检验样本来自正态分布的原假设与样本不来自正态分布的备择假设。在本例中,检验的 p 值为0.005999 ,低于 alpha 水平 0.05。这表明样本不服从正态分布。
如果不遵守此假设该怎么办:
一般来说,只要样本量足够大,单向方差分析就被认为对于违反正态性假设非常稳健。
此外,如果您有非常大的样本,像夏皮罗-威尔克检验这样的统计检验几乎总是会告诉您您的数据不正常。因此,通常最好使用直方图和 QQ 图等图表来直观地检查数据。只需查看图表,您就可以很好地了解数据是否服从正态分布。
如果正态性假设被严重违反或者你只是想非常保守,你有两种选择:
(1)变换数据的响应值,使分布更加正态分布。
(2)执行等效的非参数检验,例如不需要正态性假设的Kruskal-Wallis 检验。
假设#2:方差相等
方差分析假设从中抽取样本的总体的方差是相等的。
如何在 R 中检验这个假设:
我们可以使用两种方法在 R 中验证这个假设:
- 使用箱线图直观地验证假设。
- 使用正式的统计检验(例如巴特利特检验)来检验假设。
以下代码演示了如何使用我们之前创建的相同的假减肥数据集来执行此操作。
1. 创建箱线图。
#Create box plots that show distribution of weight loss for each group boxplot(weight_loss ~ program, xlab=' Program ', ylab=' Weight Loss ', data=data)
每组体重减轻的方差可以通过每个箱线图的长度来观察。盒子越长,方差就越大。例如,我们可以看到,与计划 A 和计划 B 相比,计划 C 的参与者的方差稍高一些。
2. 执行巴特利特检验。
#Create box plots that show distribution of weight loss for each group bartlett. test (weight_loss ~ program, data=data) #Bartlett test of homogeneity of variances # #data: weight_loss by program #Bartlett's K-squared = 8.2713, df = 2, p-value = 0.01599
Bartlett 检验测试样本具有相等方差的原假设与样本不具有相等方差的备择假设。在本例中,检验的 p 值为0.01599 ,低于 alpha 水平 0.05。这表明样本并不都具有相同的方差。
如果不遵守此假设该怎么办:
一般来说,只要每组具有相同的样本量,单向方差分析就被认为对于违反等方差假设相当稳健。
但是,如果样本大小不相同并且严重违反了这一假设,您可以改为运行Kruskal-Wallis 检验,这是单向方差分析的非参数版本。
假设#3:独立性
方差分析假设:
- 每组的观察结果独立于所有其他组的观察结果。
- 每组内的观察结果是通过随机样本获得的。
如何验证这个假设:
没有正式的测试可以用来验证每组中的观察结果是独立的并且它们是通过随机样本获得的。满足这一假设的唯一方法是使用随机设计。
如果不遵守此假设该怎么办:
不幸的是,如果不满足这个假设,你就无能为力。简而言之,如果收集数据的方式使得每组中的观察结果不独立于其他组中的观察结果,或者每组中的观察结果不是通过随机过程获得的,则方差分析结果将不可靠。
如果不满足此假设,最好的办法是使用随机设计重新创建实验。
进一步阅读:
