如何分析方差分析模型中的残差
ANOVA （“方差分析”）是一种模型，用于确定三个或更多独立组的平均值之间是否存在显着差异。
我们将方差分析拟合到数据集上时，总会有残差——这些残差代表每个单独的观察值与观察值来源的组平均值之间的差异。
以下示例展示了如何在实践中计算方差分析模型的残差。
示例：方差分析中残差的计算
假设我们招募 90 人参加减肥实验，随机分配 30 人遵循方案 A、方案 B 或方案 C 一个月。
我们可以进行单向方差分析，以确定这三个计划所带来的体重减轻是否存在统计上的显着差异。
假设我们计算参加每个项目的个人的平均体重减轻如下：
- 方案A ：1.58磅
- 方案 B ：2.56 磅
- 方案C ：4.13磅
方差分析模型的残差将是每个人的体重减轻与其计划的平均体重减轻之间的差异。
例如，下表显示了如何计算研究中 10 个不同个体的残差：
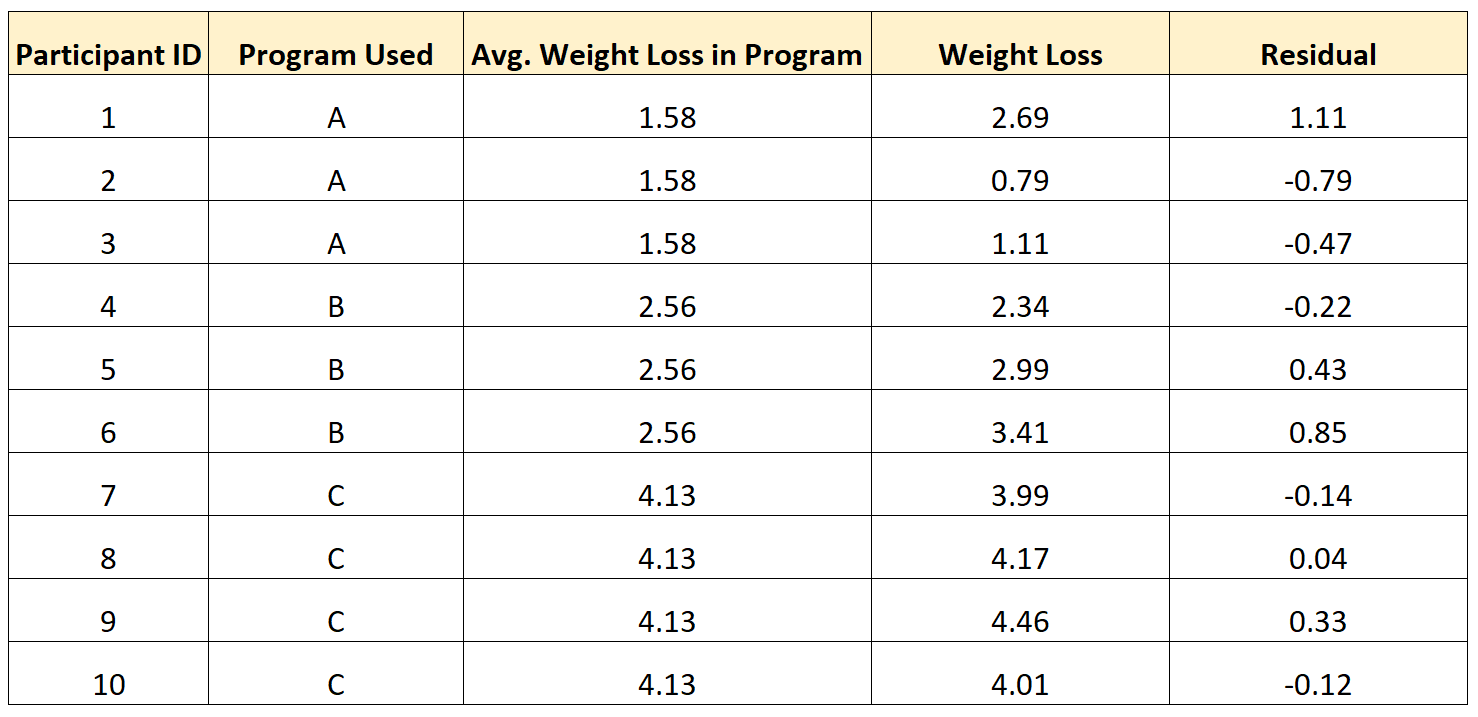
请注意以下模式：
- 数值高于群体平均水平的个体具有正残差。
- 值低于其群体平均值的个体具有负残差。
实际上，我们会计算所有 90 个人的残差。
如何使用残差检查正态性
方差分析的假设之一是残差呈正态分布。
验证这一假设的最常见方法是创建QQ 图。
如果残差呈正态分布，则 QQ 图上的点将位于直线对角线上。
对于我们之前的示例，QQ 图如下所示：
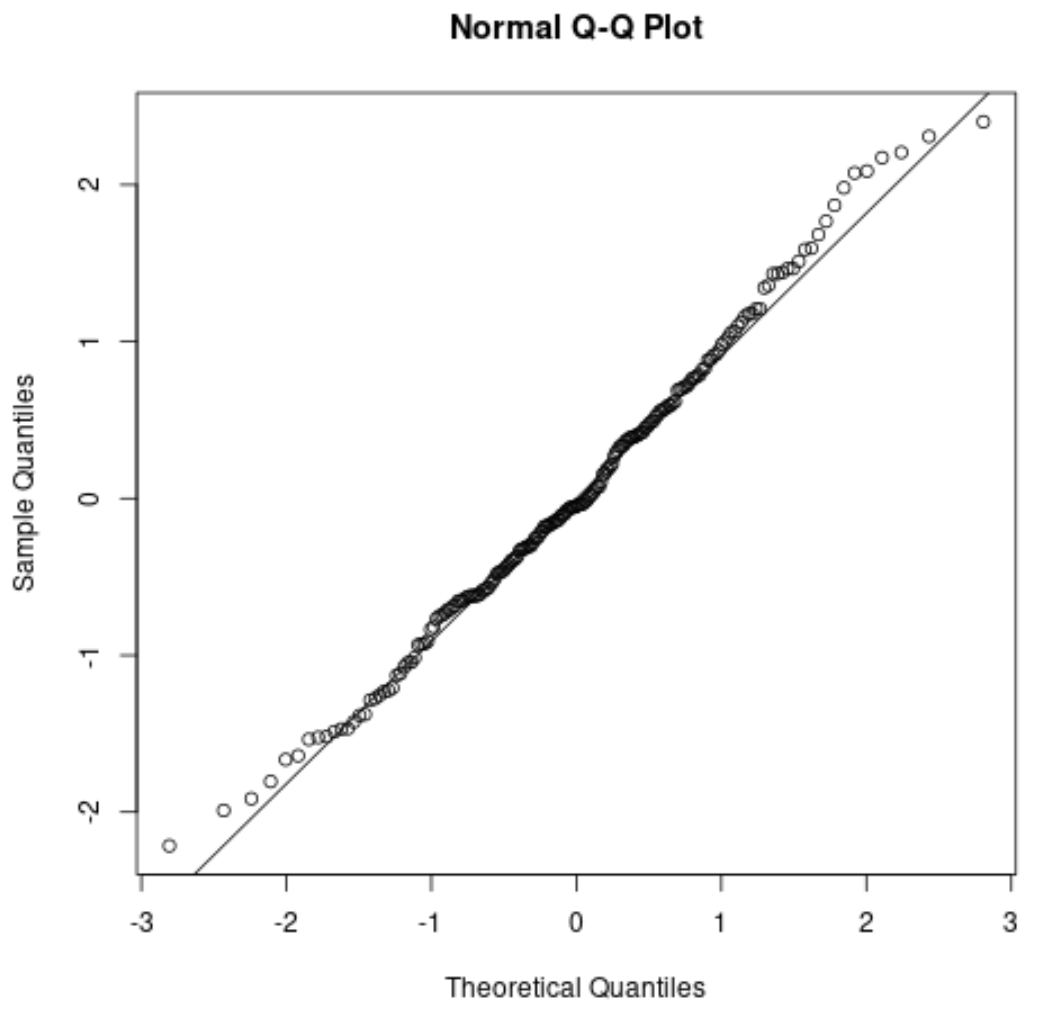
尖端稍微偏离尾部末端的直线对角线，但总的来说，尖端很好地沿着对角线落下。这告诉我们可能满足正态性假设。
作为参考，非正态分布残差的 QQ 图可能如下所示：
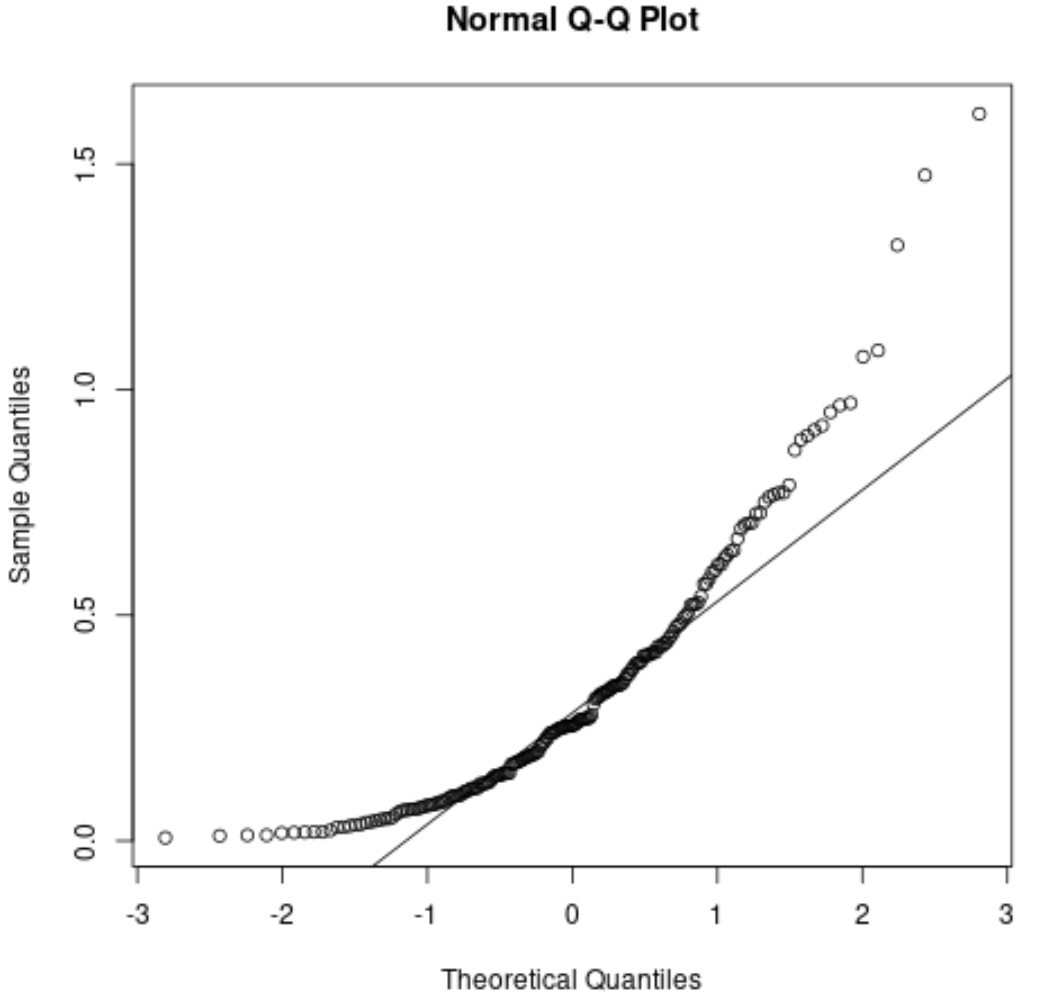
这些点与直线对角线偏离很大，表明残差不服从正态分布。
参考以下教程，了解如何在不同软件中创建QQ图：
其他资源
以下文章提供了有关 ANOVA 模型的其他信息：
关于作者
本杰明·安德森博
大家好，我是本杰明，一位退休的统计学教授，后来成为 Statorials 的热心教师。 凭借在统计领域的丰富经验和专业知识，我渴望分享我的知识，通过 Statorials 增强学生的能力。了解更多