如何计算连续变量和分类变量之间的相关性

当我们要计算两个连续变量之间的相关性时，我们一般使用皮尔逊相关系数。

然而，当我们想要计算连续变量和分类变量之间的相关性时，我们可以使用所谓的点双列相关性。

点双列相关用于计算二元分类变量（只能取两个值的变量）与连续变量之间的相关性，具有以下性质：

• 点双列相关性可以在 -1 和 1 之间变化。
• 对于由二元变量创建的每个组，假设连续变量服从等方差正态分布。
• 对于由二元变量创建的每个组，假设不存在极端异常值。

以下示例展示了如何在实践中计算点双列相关性。

示例：点双列相关性的计算

假设一位大学教授想要确定性别和特定资格考试成绩之间是否存在相关性。

他收集了班上 12 个男孩和 12 个女孩的以下数据：

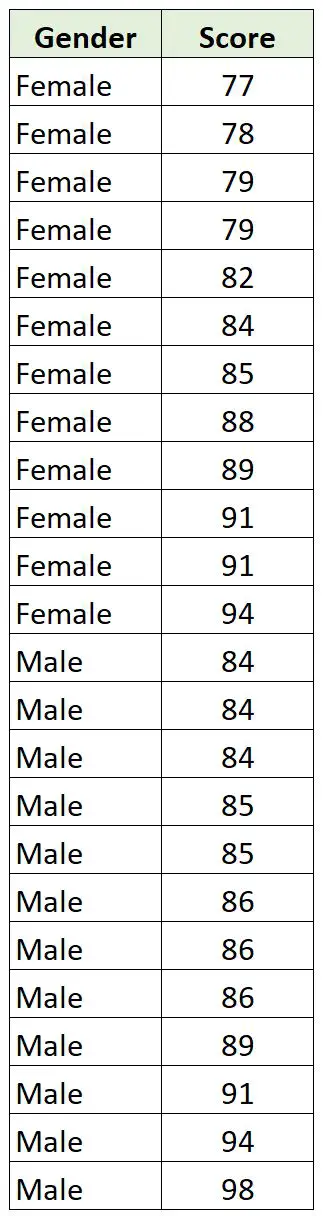
由于性别是分类变量而分数是连续变量，因此计算两个变量之间的点二列相关性是有意义的。

教授可以使用任何统计软件（包括Excel、R、Python、SPSS、Stata）来计算两个变量之间的点二列相关性。

以下代码显示了如何在 R 中计算点二列相关性，使用值 0 代表女性，使用 1 代表性别变量的男性：

 #define values for gender
gender <- c(0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
            1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1)

#define values for score
score <- c(77, 78, 79, 79, 82, 84, 85, 88, 89, 91, 91, 94,
           84, 84, 84, 85, 85, 86, 86, 86, 89, 91, 94, 98)

#calculate point-biserial correlation
horn. test (gender, score)

	Pearson's product-moment correlation

data: gender and score
t = 1.3739, df = 22, p-value = 0.1833
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 -0.1379386 0.6147832
sample estimates:
      horn 
0.2810996

从结果中，我们可以看到点双列相关系数为0.281 ，相应的 p 值为0.1833 。

由于相关系数为正，这告诉我们性别和分数之间存在正相关关系。

由于我们将男性编码为 1，女性编码为 0，这表明男性的分数往往较高（即分数往往随着性别“增加”而增加）。 » 从 0 到 1）。

然而，由于 p 值不小于 0.05，因此该相关系数在统计上不显着。

其他资源

以下教程解释了如何使用不同的统计软件计算点双列相关性：

如何在 Excel 中计算点二列相关性
如何计算 R 中的点双列相关性
如何在 Python 中计算点双列相关性