统计学中连续性校正的简单解释
当您想要使用连续分布来近似离散分布时,将应用连续性校正。通常,当您想要使用正态分布来近似二项式分布时,会使用它。
回想一下,二项式分布告诉我们在n 次试验中取得x成功的概率,假设单次试验成功的概率为p 。要回答有关二项分布概率的问题,我们可以简单地使用二项分布计算器,但我们也可以使用具有连续性校正的正态分布来近似概率。
连续性校正是指从离散 x 值中加上或减去 0.5 。
例如,假设我们想要计算一枚硬币在 100 次抛掷过程中正面朝上的概率小于或等于 45 次。也就是说,我们要找到 P(X ≤ 45)。要使用正态分布来近似二项式分布,我们需要找到 P(X ≤ 45.5)。
下表显示了何时应该添加或减去 0.5,具体取决于您尝试查找的概率类型:
| 使用二项式分布 | 使用具有连续性校正的正态分布 |
|---|---|
| X = 45 | 44.5 < X < 45.5 |
| X≤45 | X < 45.5 |
| X < 45 | X < 44.5 |
| X≥45 | X > 44.5 |
| X > 45 | X > 45.5 |
笔记:
仅当 n*p 和 n*(1-p) 都至少为 5 时,才适合对正态分布应用连续性校正以近似二项式分布。
例如,假设 n = 15 且 p = 0.6。在这种情况下:
n*p = 15 * 0.6 = 9
n*(1-p) = 15 * (1 – 0.6) = 15 * (0.4) = 6
由于这两个数字都大于或等于 5,因此在这种情况下应用连续性校正是可以接受的。
以下示例说明如何对正态分布应用连续性校正以逼近二项式分布。
连续性校正的应用示例
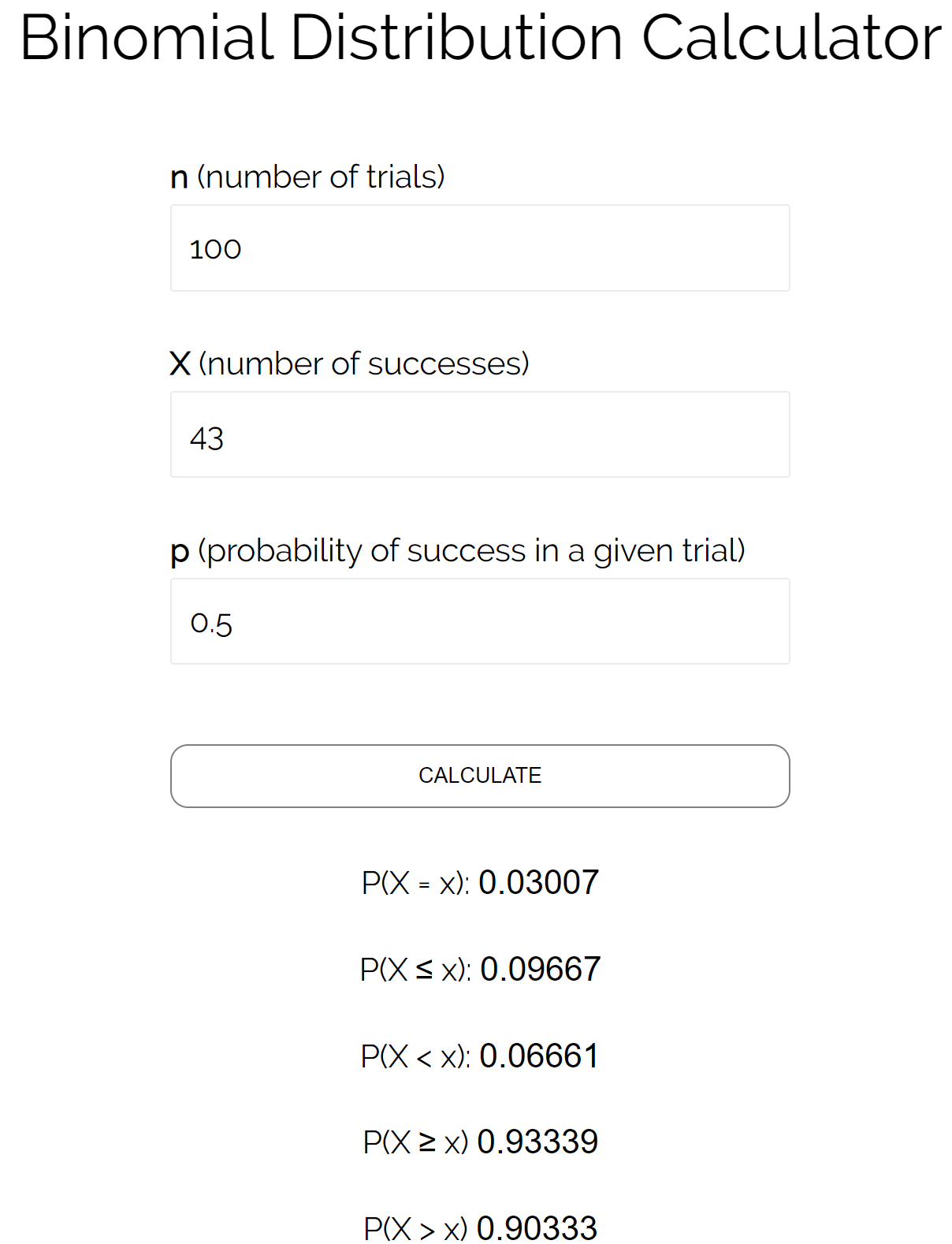
假设我们想知道抛掷 100 次硬币,正面朝上的次数少于或等于 43 次的概率。在这种情况下:
n = 试验次数 = 100
X = 成功次数 = 43
p = 给定试验的成功概率 = 0.50
我们可以将这些数字代入二项式分布计算器,可以看到硬币正面朝上的次数小于或等于 43 次的概率为0.09667 。
要通过对正态分布应用连续性校正来近似二项式分布,我们可以使用以下步骤:
步骤 1:验证 n*p 和 n*(1-p) 都至少为 5 。
n*p = 100*0.5 = 50
n*(1-p) = 100*(1 – 0.5) = 100*0.5 = 50
两个数字都大于或等于 5,所以我们可以继续。
步骤2:确定是加还是减0.5
参考上表,我们看到当我们处理 X ≤ 43 形式的概率时,我们应该加上0.5 。因此,我们会找到 P(X< 43.5)。
步骤 3:求二项式分布的均值 (μ) 和标准差 (σ)。
µ = n*p = 100*0.5 = 50
σ = √ n*p*(1-p) = √ 100*.5*(1-.5) = √ 25 = 5
步骤 4:使用上一步中找到的平均值和标准差求出 z 分数。
z = (x – μ) / σ = (43.5 – 50) / 5 = -6.5 / 5 = -1.3。
步骤 5:使用 Z 表查找与 z 分数相关的概率。
根据表 Z,与 z = -1.3 相关的概率为0.0968 。
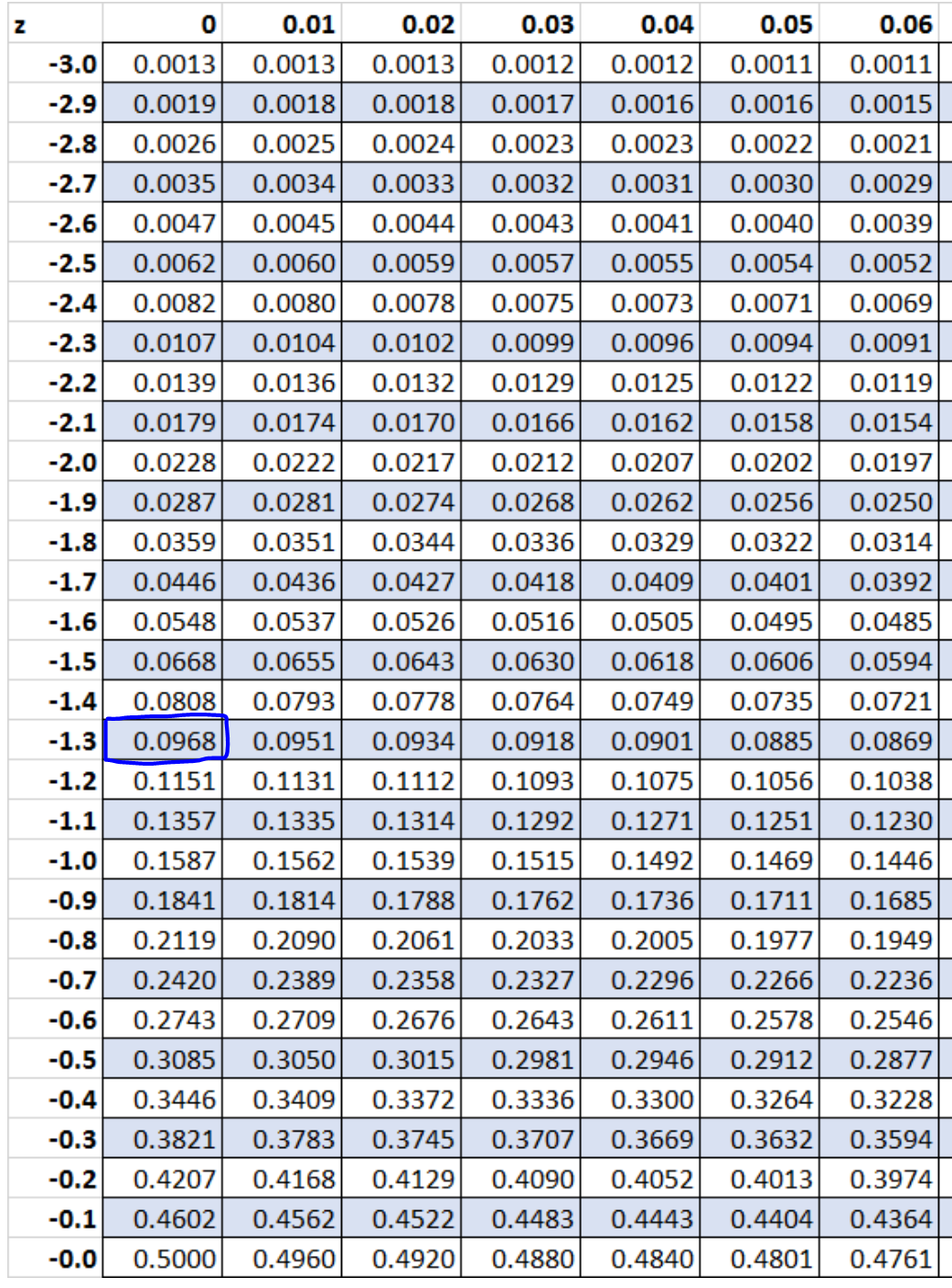
因此,我们使用二项分布发现的精确概率是0.09667 ,而我们使用正态分布的连续性校正发现的近似概率是0.0968 。这两个值相当接近。
何时使用连续性校正
在现代统计软件出现并且计算必须手动完成之前,连续性校正通常用于查找涉及离散分布的概率。如今,连续性修正在计算概率中发挥的作用越来越小,因为我们通常可以依靠软件或计算器来计算概率。
相反,它只是统计学课程中涵盖的一个主题,用于说明二项式分布和正态分布之间的关系,并表明正态分布可以通过应用连续性校正来逼近二项式分布。
连续性校正计算器
使用连续性校正计算器自动将连续性校正应用于正态分布以近似二项式概率。